Switch to the geometric tab using the ![]() button.
button.
We will create an equilateral triangle which side length is a and calculate its altitude.
In the geometric tab menu, choose Create Object then Point and Coordinated Point (Create Object / Point / Coordinated Point).
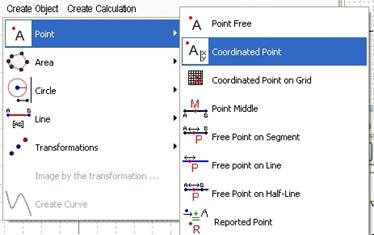
Figure 17 - Menu Create Object / Point / Coordinated Point
A dialogue box opens, for x enter 0 and for y, a. Click on Create and Exit.
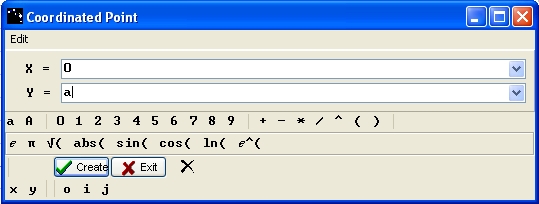
Figure 18 - Coordinated point creation box
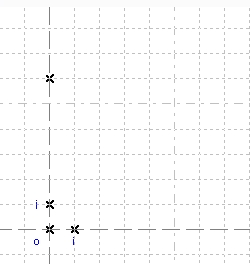
Figure 19 - First point in geometry tab
To name a point, right-click on it. A box opens, with the drop down menu, you can choose a letter name and you can choose the name’s position. Name the new point B.
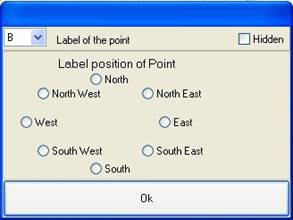
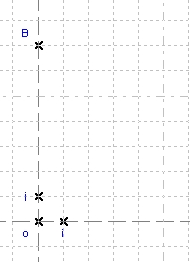
Figure 20 - Point properties box Figure 21 - Point B
We will create two circles: Create Object / Circle / Circle by Center and passing through a Point. The first circle is by centre o and passing through the point B, the second is by centre B and passing through the point o.
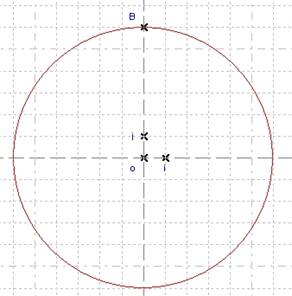
Figure 22 - First circle Figure 23 - Second circle
Now we will create the two circle intersection points: Create Object / Point / Intersection of two Circles. Select one of the circles then the second. It creates the two points. Name them C and D.
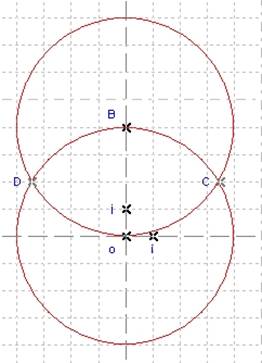
Figure 24 - Intersection points C and D
We will create the segment [oB]: Create Object / Line / Segment. Select the point o or B then the other point. It creates the segment.
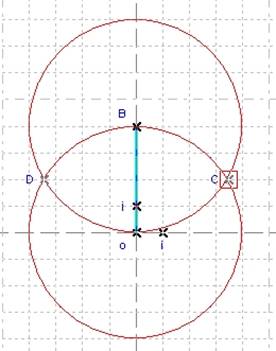
Figure 25 - Segment [oB]
Create the point middle H of segment [oB]: Create Object / Point / Point Middle. Select the segment [oB]. Name the point H.
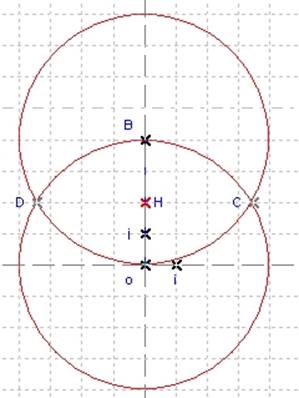
Figure 26 - Middle point H
Switch to the geometric calculation tab (![]() button).
button).
Consider the BoC triangle. Each radius circle measures a, so Bo, oC and CB measure a. Boc is an equilateral triangle. To measure its altitude: CH, create the geometric calculation CH. Click on Create Calculation. In the box, in Calculation box enter CH. Click on Create then Exit.
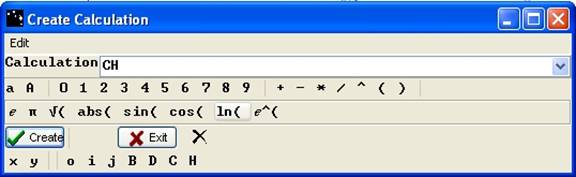
Figure 27 - Creation of geometric calculation CH
In the geometric calculation tab, Casyopée created the calculation c0. When one checks the calculation, one can observe an approximate value. How does this value depend on a?
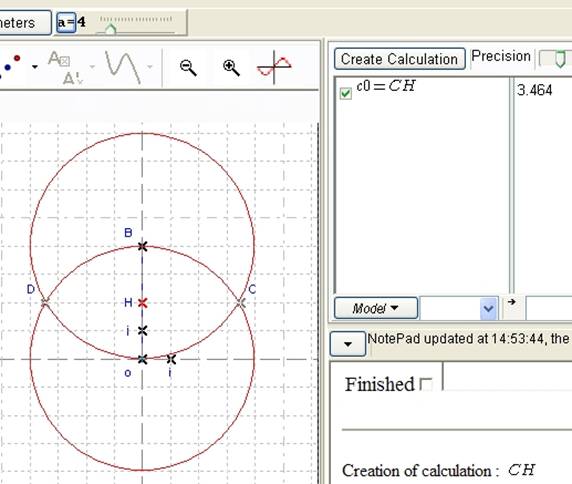
Figure 28 - Figure and calculation when a = 4
In the toolbar, change the value of a. Observe that circles’ radius and the resulting change of c0.
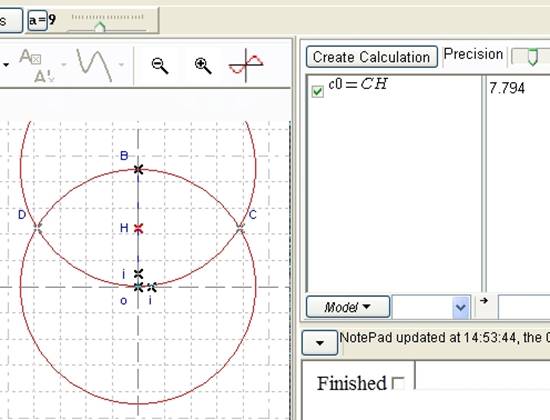
Figure 29 - Figure and calculus when a = 9
The value of CH could depend on a. To verify this hypothesis, highlight the calculation, choose Dependance. A box opens, it says that “The calculation depends on no free point” and suggests to export as an expression. Choose Yes.
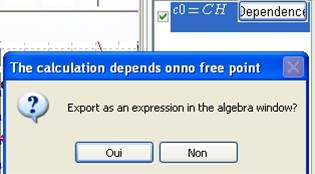
Figure 30 - Calculation exportation box
Another box opens and gives the new geometrical expression. It is depending on a. Click on OK.
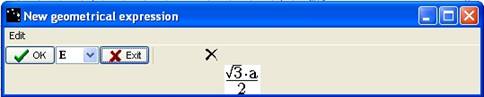
Figure 31 - Box "New geometrical expression"
Go back into the expression list (with ![]() button), observe the new expression E, which gives the altitude of an equilateral triangle whose side is a.
button), observe the new expression E, which gives the altitude of an equilateral triangle whose side is a.

Figure 32 - Expression E of the altitude of an equilateral triangle whose side is a
Category : -
Page read 7950 times




