Determining the sign of a linear function
Determining the variations of a linear function.
Justifying sign from variations
Determining the sign of a product
We take the example of the sign of the product of two linear expressions.
Two ways for determining the sign of a linear expression are demonstrated:
- one uses results about linear expressions' sign (method 1),
- the other uses results about variation of linear functions (method 2).
Then we will use the rule of signs of a product or of a quotient for the signs of f.
Finding sub-expressions
Create the function f . You can use function by formula. However, it is important to check the domain in order that the mini-diagram appear. In the expressions list, click on the expression of f.
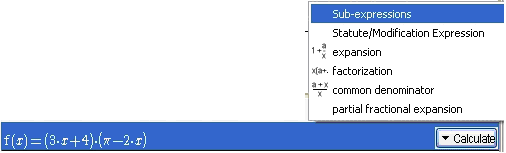
Figure 62 - Menu Calculate / Sub-expression
Click on the Calculate button, in the contextual menu which appears, choose Sub-expressions. The following box appears, it lists the sub-expressions.
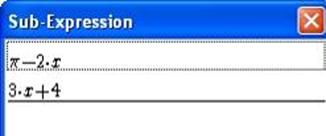
Figure 63 - Sub-expressions list
The selection of list's elements is as in Windows™ explorer :
Keeping « Ctrl » key pressed, click on non-consecutive elements in order to select them.
Keeping « Shift » or ![]() key pressed, click on first, then on last element of the list to be selected; the All button selects all the elements.
key pressed, click on first, then on last element of the list to be selected; the All button selects all the elements.
In this example choose All, then click OK. The expressions and functions lists are completed by two functions named f0 and f1 defined from the selected expressions.
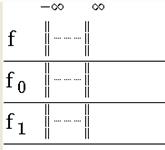
Figure 64 - Sub-expressions (functions list)

Figure 65 - Sub-expressions (expressions list)
Determining the sign of a linear function
Highlight f1 in the functions list as seen above.
In the Justify menu, choose Sign: linear.
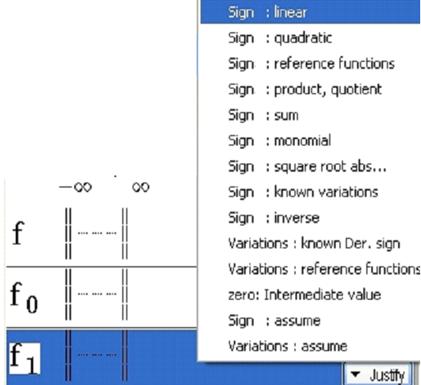
Figure 66 - Menu Justify / Sign - linear
A dialog box appears.
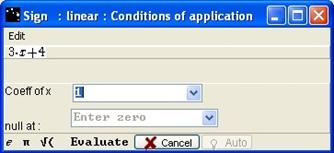
Figure 67 - Box "Sign - linear - Condition of application"
Fill in Coeff of x and null at then click on the Evaluate button. If there is an error, information appears in the Notepad.
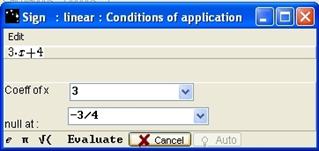
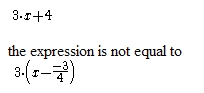
Figure 68 - Sign linear completed box with error
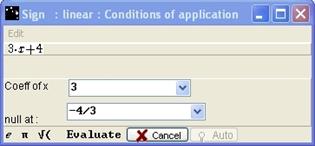
Figure 69 - Box with correct answer
If the correct values are entered, after clicking Evaluate, a new box opens.
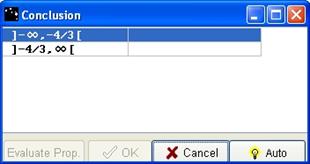
Figure 70 - Conclusion box for the sign of linear function
On each line, successive clicks in the blank box make negative or positive appear; evaluate your propositions by clicking the Evaluate Prop button.
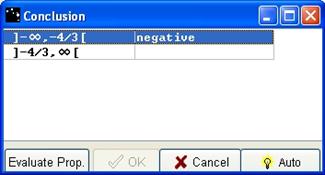
Figure 71 - Conclusion box with first line filled
When propositions are correct, the OK button is active, please press it.
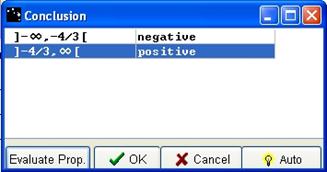
Figure 72 - Conclusion box with correct answers
The zero of f1 is added in the x-values list and in the functions list the sign of f1 is showed with green bullets (positive if the bullet is above the horizontal line passing by 0, else negative).
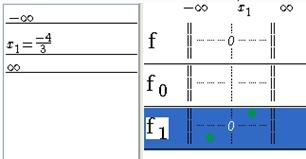
Figure 73 - Displaying sign of f1
Determining the variations of a linear function
In order to determine the sign of (π – 2x), create the zero of the expression f0 (π/2) in the x-value list (click New Value) then select f0 in the functions list.
In the Justify menu, choose Variations: reference functions.
Figure 74 - Menu Justify / Variations - reference functions
This box opens:
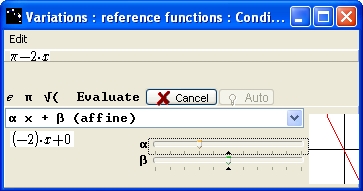
Figure 75 - Box "Variations - reference functions - Conditions of application"
You can choose the type of function in the list, and you will get a graphical representation of the chosen function’s type. Click on Evaluate.
After a correct answer, a Conclusion box opens.
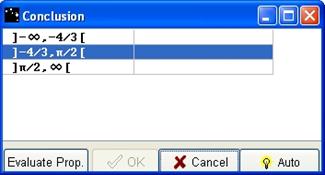
Figure 76 - Conclusion box for variations
For each line, click on the blank box in order to make decreasing or increasing appear. Evaluate your propositions with the Evaluate Prop button. When propositions are correct, the OK button is active, please press it.
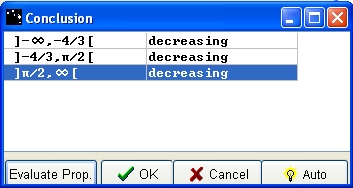
Figure 77 - Conclusion box for variations with correct answers.
In the functions list, results appear in the mini-diagrams (arrows).

Figure 78 - Displaying variations of f0
Justifying sign from variations
After variations, it is needed to justify the sign; in the Justify menu, choose Sign: known variations.
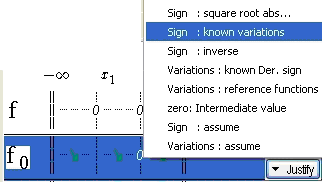
Figure 79 - Menu Justify / Sign - known variations
The box Sign: Known variations: application conditions opens. At one of the values in the drop down menu, indicate if the function is negative, zero or positive. Here, choose x2 and zero function. It means that you recognised that the function is decreasing and null at x2, and then Casyopée will know that the function is positive for x< x2 and negative for x> x2. When the proposition is correct, the Evaluate button is active, please press it.
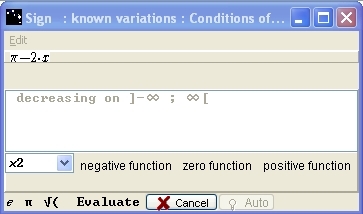
Figure 80 - Box "Sign - known variations - Conditions of application"
A Conclusion box opens. For each line, click on the blank box in order to make negtive or positive appear. Evaluate your propositions with the Evaluate Prop button. When propositions are correct, the OK button is active, please press it.
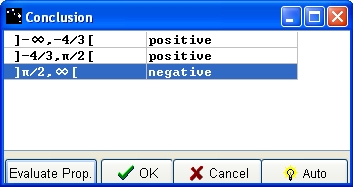
Figure 81 - Conclusion box for sign of a function with known variations
The signs of f0 are denoted by the position of arrows. Above the line passing by 0, the function is positive and under, the function is negative.
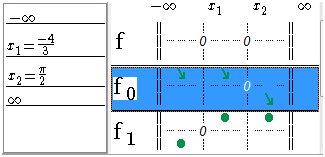
Figure 82 – Sign diagram of f0
Determining the sign of a product
Finally, in the functions list, select f, and then click on the Justify menu, choose Sign: product, quotient.
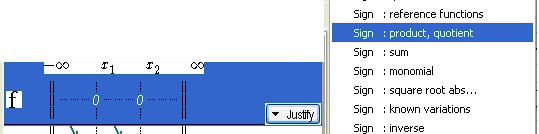
Figure 83 - Menu Justify / Sign - product, quotient
At the bottom of the dialogue box, select the two lines, because f is the product of f0 and f1.
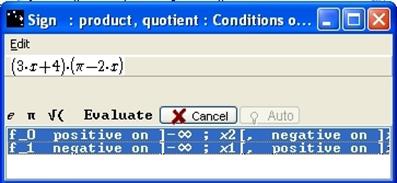
Figure 84 - Box "Sign - product, quotient - Conditions of application"
Click on Evaluate, the Conclusion box opens. The meaning of this window has already been explicated. After pressing Evaluate Prop. and OK, the results appear as signs in the functions list.
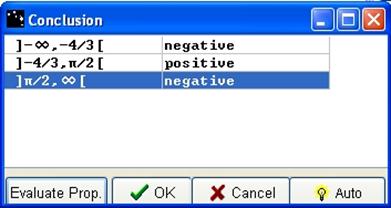
Figure 85 - Conclusion box for the sign of a product
In the functions list, the table of sign is totally filled. The Notepad allows to keep track of the different steps and to write a justification.
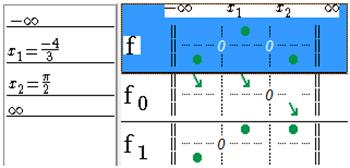
Figure 86 - Sign table of functions
Category : - help
Page read 10657 times




