Connecting rod and crank mechanism
Consider M a mobile point on the circle centred in o with radius one and P the point on the half-line [ox) such as MP is constant (equal to a, a being a positive parameter). We want to model the dependency between the distance oP and the position of M over the circle. For mechanics, [oM] is part of the crank and [MP] is the connecting rod.
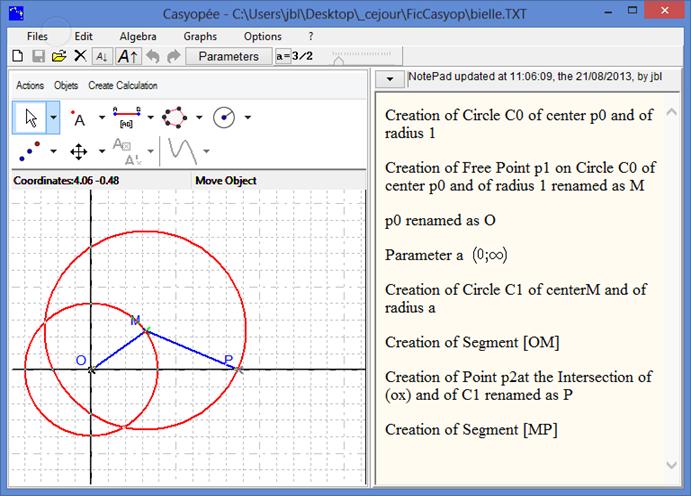
Figure 101 - Connecting rod and crank mechanism
Follow the construction in the NotePad Figure 101. You may assign a speed to point M in order to animate the mechanism (see p. 11). Stop by Action Stop Mobile Points.
To model the mechanism, OP is obviously the dependent variable to choose. But, what might we choose an independent variable? We can create the angle between the x-axis and OM that varies while M is moving on the circle. Click the angle button  and then a point on the axis (choosing fixed point in the menu), O and M.
and then a point on the axis (choosing fixed point in the menu), O and M.
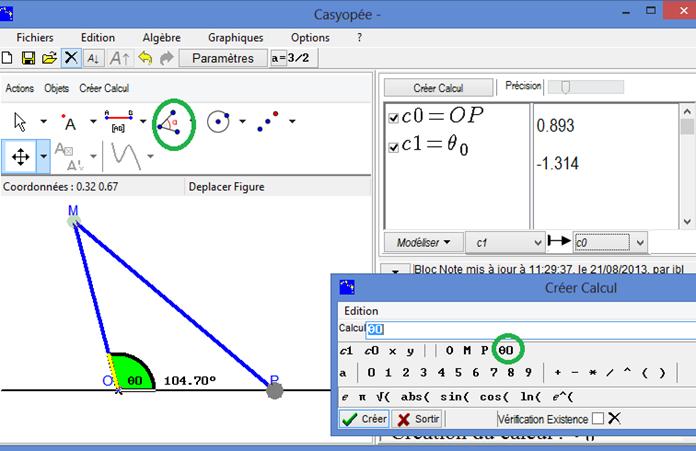
Figure 102 - Creating calculations (distance and angle)
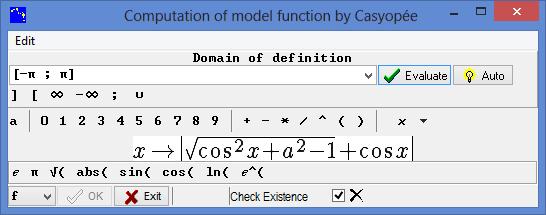
Figure 103 - domain and formula of the model function
After asking Casyopée to compute the function by way of the model menu, you evaluate the domain and confirm (OK). If you asked to check existence, you get a message warning that Maxima cannot guaranty that the definition is mathematically correct.
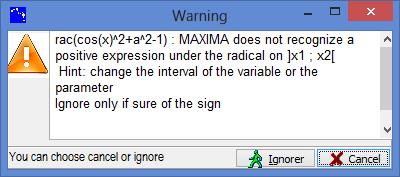
Figure 104 - Casyopée's warning
Note that such warning can happen whereas the definition is correct; it is because of symbolic computation limits. That is why you can ignore the warning. After a new warning the function can be created.
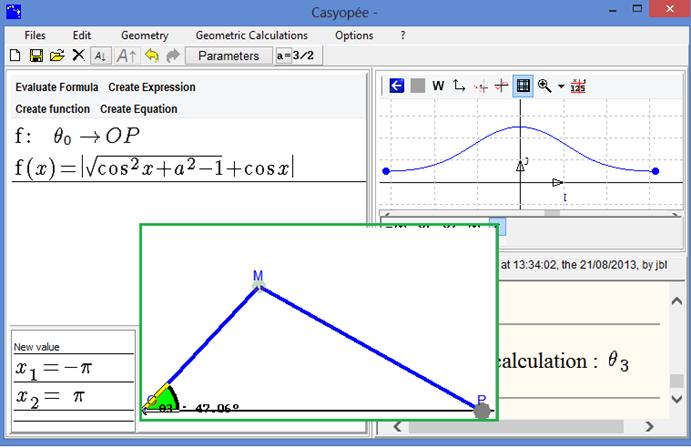
Figure 105 - Rod and crank, model function
Note also that the reverse dependency (c0 -> c1) does not work because for one value of OP correspond two values of the angle. The diagnostic will be: The calculation depends on M. Casyopée cannot compute a model function with the independent variable c0.
cool wink biggrin smile frown eek mad confused rolleyes tongue cry Enregistrer => Retour Tous les articles Courriel admins ^ Haut ^ Vous êtes ici : Accueil » Admin » Gérer les articles DECONNEXION freeguppy.org © 2004-2014 En savoir plus ... Langue: en Casyopée => [admin] Vous êtes ici : Accueil » Admin » Gérer les articles DECONNEXION Généralités A propos Version de GuppY Aide Mot de passe Admin Travaux Configurations Config générale Config services Config sections Config contact Config Recherche Config thèmes Config look Config boîtes Config accueil Config Style Administration générale Config zone membres Gestion des groupes Gestion des membres Ecrire aux membres Attribution de Droits Gestion des collaborateurs Gestion des groupes de collaborateurs Contrôle d'intégrité DB Maintenance Archivage des Données Installer Sauvegarder Import Doc. Fichiers Compteur visites Compteur articles Compteur forum Compteur téléchargements Voir les statistiques Purger les statistiques Configurer les statistiques Définitions de bannissement Paramètres de bannissement Voir les journaux de bannissement Définitions de black-listage Paramètres de black-listage Voir les journaux de black-listage Config générale Log Voir le fichier Log Structure Boîtes libres Documents RSS Bannières Citations Sondage Menu Icônes Boîtes menus Options de menu Boîtes menus déroulants Options de menu déroulant Code réseau social pour les services Créer des accès réseaux sociaux Administration des données Articles Réactions Articles Téléchargements Liens FAQ Liste des abonnés Gestion des groupes Ecrire une lettre d'information Envoyer une lettre d'information Envoyer une nouvelle Admin - Gérer les articles Aide Gérez ici vos articles. Astuce : les articles sont triés par titre, toujours par ordre alphabétique. Aussi vous pouvez les numéroter (exemple: Titre) pour les ranger dans l'ordre que vous souhaitez. Tous les articles || Ecrire un article Enregistrer => Retour Tous les articles Ne pas modifier la date de mise à jour Courriel admins Accès réservé au groupe privé : -- Non -- Tous les membres Publication programmée Début : Fin : Pseudo du rédacteur : Groupe du rédacteur : Tous les rédacteurs Courriel du rédacteur : Titre de l'article : ../inc/lang/fr.gif ../inc/lang/en.gif Mode d'affichage des boîtes latérales standard sans aucune colonne toutes les boîtes dans la colonne gauche toutes les boîtes dans la colonne droite Icône de l'article : Mots-clés (séparés par un point-virgule) : ../inc/lang/fr.gif ../inc/lang/en.gif Ecrivez votre article : fr Source StylesNormalPoliceTaille ◢bodytabletbodytrtdpimg cool wink biggrin smile frown eek mad confused rolleyes tongue cry en Source StylesFormatPoliceTaille
Connecting rod and crank mechanism
Consider M a mobile point on the circle centred in o with radius one and P the point on the half-line [ox) such as MP is constant (equal to a, a being a positive parameter). We want to model the dependency between the distance oP and the position of M over the circle. For mechanics, [oM] is part of the crank and [MP] is the connecting rod.

Figure 101 - Connecting rod and crank mechanism
Follow the construction in the NotePad Figure 101. You may assign a speed to point M in order to animate the mechanism (see p. 11). Stop by Action Stop Mobile Points.
To model the mechanism, OP is obviously the dependent variable to choose. But, what might we choose an independent variable? We can create the angle between the x-axis and OM that varies while M is moving on the circle. Click the angle button  and then a point on the axis (choosing fixed point in the menu), O and M.
and then a point on the axis (choosing fixed point in the menu), O and M.

Figure 102 - Creating calculations (distance and angle)

Figure 103 - domain and formula of the model function
After asking Casyopée to compute the function by way of the model menu, you evaluate the domain and confirm (OK). If you asked to check existence, you get a message warning that Maxima cannot guaranty that the definition is mathematically correct.

Figure 104 - Casyopée's warning
Note that such warning can happen whereas the definition is correct; it is because of symbolic computation limits. That is why you can ignore the warning. After a new warning the function can be created.

Figure 105 - Rod and crank, model function
Note also that the reverse dependency (c0 -> c1) does not work because for one value of OP correspond two values of the angle. The diagnostic will be: The calculation depends on M. Casyopée cannot compute a model function with the independent variable c0.
cool wink biggrin smile frown eek mad confused rolleyes tongue cry Enregistrer => Retour Tous les articles Courriel admins ^ Haut ^ Vous êtes ici : Accueil » Admin » Gérer les articles DECONNEXION freeguppy.org © 2004-2014 En savoir plus ...
Connecting rod and crank mechanism
Consider M a mobile point on the circle centred in o with radius one and P the point on the half-line [ox) such as MP is constant (equal to a, a being a positive parameter). We want to model the dependency between the distance oP and the position of M over the circle. For mechanics, [oM] is part of the crank and [MP] is the connecting rod.

Figure 101 - Connecting rod and crank mechanism
Follow the construction in the NotePad Figure 101. You may assign a speed to point M in order to animate the mechanism (see p. 11). Stop by Action Stop Mobile Points.
To model the mechanism, OP is obviously the dependent variable to choose. But, what might we choose an independent variable? We can create the angle between the x-axis and OM that varies while M is moving on the circle. Click the angle button  and then a point on the axis (choosing fixed point in the menu), O and M.
and then a point on the axis (choosing fixed point in the menu), O and M.

Figure 102 - Creating calculations (distance and angle)

Figure 103 - domain and formula of the model function
After asking Casyopée to compute the function by way of the model menu, you evaluate the domain and confirm (OK). If you asked to check existence, you get a message warning that Maxima cannot guaranty that the definition is mathematically correct.

Figure 104 - Casyopée's warning
Note that such warning can happen whereas the definition is correct; it is because of symbolic computation limits. That is why you can ignore the warning. After a new warning the function can be created.

Figure 105 - Rod and crank, model function
Note also that the reverse dependency (c0 -> c1) does not work because for one value of OP correspond two values of the angle. The diagnostic will be: The calculation depends on M. Casyopée cannot compute a model function with the independent variable c0.
Category : - help
Page read 9364 times




