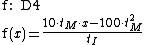Casyopee - Paramètres géométriques dans les fonctions

The site will be translated into the primary language: fr

Home
Links

What they say: I used Casyopée to help students solve optimisation problems. It allowed me to present students very open tasks. Students explored and found results that they had to prove afterward. Casyopée also helped students reuse basic strategies for solving. A teacher

What they say: Casyopée is faster and more convenient than a calculator.... We have the geometric and algebraic side of the problem at the same time. It is easier to see how a function "reacts." It's useful and interesting. A student

What they say: Casyopée makes it easy to calculate a derivative, to factor, to calculate zeros... and have a graph of the function next to it in the same window. It allows on a geometric problem to be able to establish variables that can then be used to study the problem by way of functions... A student

What they say: Casyopee is a powerful application that can prove useful to both students and teachers It allows you to use various exploration and modeling tools, with the purpose of studying or teaching mathematical functions. Softpedia

What they say: Casyopee comes with lots of features. One of these features is the help provided for proving a function. There is also a feature for writing HTML reports that include the mathematical functions. Casyopee is guaranteed to improve the mathematical knowledge of its users. phpnuke.org

What they say: Besides the concept of number, the concept of function is the most important one in mathematics David Hilbert

What they say: The notion of function is present in all scientific disciplines, and also in everyday life. Our experience as a teacher shows every day that it is a problem for many students. Situations with Casyopée can also be used outside of a technological environment and everyone will be able to reflect on her professional practice. A university teacher

Paramètres géométriques dans les fonctions

Geometrical parameters in functions

In Casyopée, functions make the connection between geometry and algebra. Thus, a function can

1. model a geometric dependency between variables

2. be a function whose graphical representation is a given line (modelling a straight line).

3. be a function whose graphical representation is the locus of a point (modelling a locus).

A limitation of versions before 3.2.1 was that the functions were "purely mathematical" which forced models to involve a minimal number of geometric data.

1. An example of modelling a geometric dependency with « Minh’s triangle »

A on the x-axis, O origin, I on the y-axis, OA = 10, OI = 5, M is a free point on [OA] and IMN is rectangle in M. We study the variations of the area of the triangle MIN.

A model function is

Now suppose that we want to study the variations for any position of the point I on the y-axis.

We redefine I as free point on the y-axis. This implies that from now on, the area of triangle depends on two parameters, one linked to the point M, the other to the point I. The formula of the model function then depends on the position of the point I.

Dragging the Point I in the Geometry window, the continuous deformation of the graph of the model function is observed.

Actually, the formula of the function depends on a Geometrical parameter tI representing the position of I on the y-axis

One can make these parameters visible in the formulas by the menu Options- Calculation and Justification-Instantiate geometrical parameters

It is then possible to explicitly instantiate geometrical parameters.

2. "Equations" of lines

The context menu of a line provides access to Equation-Export as function.

The line is the graphical representation of the resulting linear function.

Here the line depends on the two free points A on the x-axis and B on the y-axis, and therefore their parameters are in the formula.

Please note that initially Geometrical parameters are instantiated automatically.

3. Locus

In previous versions, it was possible to obtain the locus of a point only if it depended of one free point parameter (eg the parameter of a free point on object).

Example: Construction of a parabola by focus and directrix.

Creation of free Point p1 on (oy) renamed F

Creation of p2 image of point F by symmetry of centre p0

Creation of Parallel D2 to (ox) passing through p2

Creation of free Point p3 on D2 renamed H

Creation of the Parallel D3 to (oy) passing through point H

Creation of Middle Point p4 of Segment [FH]

Creation of Segment [FH]

Creation of Perpendicular D4 to [FH] and passing through p4

Creation of the Intersection of D4 and D3, p5 renamed M

With the button in the line menu, clicking M then H, the function is created and the parabola is displayed.