Geometrical parameters in functions
In Casyopée, functions make the connection between geometry and algebra. Thus, a function can
1. model a geometric dependency between variables
2. be a function whose graphical representation is a given line (modelling a straight line).
3. be a function whose graphical representation is the locus of a point (modelling a locus).
A limitation of versions before 3.2.1 was that the functions were "purely mathematical" which forced models to involve a minimal number of geometric data.
1. An example of modelling a geometric dependency with « Minh’s triangle »
|
A on the x-axis, O origin, I on the y-axis, OA = 10, OI = A model function is Now suppose that we want to study the variations for any position of the point I on the y-axis. We redefine I as free point on the y-axis. This implies that from now on, the area of triangle depends on two parameters, one linked to the point M, the other to the point I. The formula of the model function then depends on the position of the point I. Dragging the Point I in the Geometry window, the continuous deformation of the graph of the model function is observed. Actually, the formula of the function depends on a Geometrical parameter tI representing the position of I on the y-axis One can make these parameters visible in the formulas by the menu Options- Calculation and Justification-Instantiate geometrical parameters
It is then possible to explicitly instantiate geometrical parameters. |
|
2. "Equations" of lines
|
The context menu of a line provides access to Equation-Export as function. The line is the graphical representation of the resulting linear function. Here the line depends on the two free points A on the x-axis and B on the y-axis, and therefore their parameters are in the formula.
Please note that initially Geometrical parameters are instantiated automatically. |
|
3. Locus
|
In previous versions, it was possible to obtain the locus of a point only if it depended of one free point parameter (eg the parameter of a free point on object). Example: Construction of a parabola by focus and directrix. Creation of free Point p1 on (oy) renamed F Creation of p2 image of point F by symmetry of centre p0 Creation of Parallel D2 to (ox) passing through p2 Creation of free Point p3 on D2 renamed H Creation of the Parallel D3 to (oy) passing through point H Creation of Middle Point p4 of Segment [FH] Creation of Segment [FH] Creation of Perpendicular D4 to [FH] and passing through p4 Creation of the Intersection of D4 and D3, p5 renamed M With the Dragging F, changes excentricity. Please note that initially Geometrical parameters are instantiated automatically. |
|






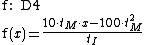




 Preview
Preview
 Print...
Print...


