On souhaite définir la fonction de répartition de la loi normale gaussienne centrée et connaître la valeur critique pour le seuil de 0,95
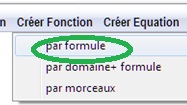
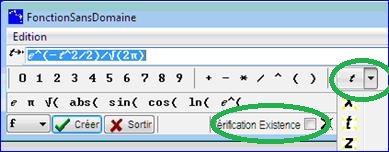
Nous allons utiliser le premier item par formule de l’entrée Créer fonction du menu de l’onglet d’Algèbre. A la différence de la Figure 3 : Boite de création des expressions, la boîte de dialogue comporte un bouton permettant d’entrer un identificateur de variable. Notez que plusieurs identificateurs sont possibles, x étant proposé par défaut. Notez aussi que comme pour les pour les expressions, il est possible de demander à Casyopée de vérifier si la fonction ainsi créée est bien définie pour tous les réels (case à cocher Vérification Existence).
|
|
|
|
Figure 33 : Créer fonction par formule |
|
La fonction étant définie, le bouton Calculer donne accès à trois calculs supplémentaires, spécifiques des fonctions. Nous essayons ici le calcul « primitive » qui donne à une constante près la fonction de répartition de la loi normale gaussienne centrée. Comme la primitive obtenue s’annule en zéro, nous définissons une fonction g en ajoutant ½ (Créer fonction, par formule, puis entrer la formule 1/2+If(t)).
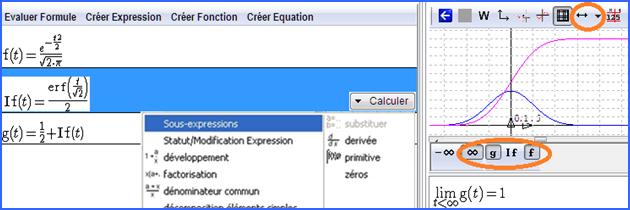
Figure 34: calculer et grapher
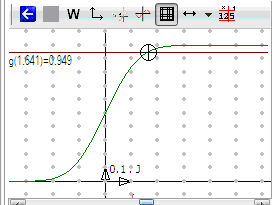
Notez les boutons en bas de la fenêtre graphique qui permettent de grapher les fonctions et d’obtenir les limites aux bornes. Dans la barre d’outils en haut, plusieurs types de zoom sont accessibles par un seul bouton. Ici pour cadrer correctement la fonction il a été nécessaire d’opérer plusieurs zoom in en y et un zoom in en x. On a aussi déplacé les axes en tirant simplement le graphique à la souris. Il aurait été aussi possible aussi de cadrer en entrant des données numériques par le bouton W. On tabule les fonctions à l’aide du bouton ![]() . Le bouton
. Le bouton ![]() permet de copier la table dans le presse- papier (séparateurs : tabulation et saut de ligne). Il est alors possible de coller les valeurs dans un traitement de texte ou un tableur.
permet de copier la table dans le presse- papier (séparateurs : tabulation et saut de ligne). Il est alors possible de coller les valeurs dans un traitement de texte ou un tableur.
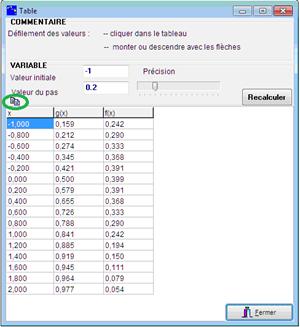
Figure 35 : tabuler une fonction
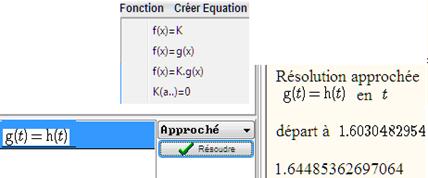
Approchons la valeur critique de la loi normale gaussienne centrée pour le seuil de 0,95. Pour une étude graphique, on peut entrer une fonction constante h et pointer sur l’intersection des graphes pour faire apparaître un curseur et des valeurs approchées. Casyopée offre aussi la possibilité d’entrer l’équation en t, g(t)=h(t) et de résoudre en mode exact ou approché. Une nouvelle liste s’ouvre en bas à gauche : c’est la liste des équations. Le mode approché s’impose ici. Casyopée applique la méthode de Newton avec comme point de départ la position du curseur.
|
|
|
Figure 36 : résolution graphique et résolution approchée
Catégorie : - aide
Page lue 11883 fois