Créer des expressions provenant de situations géométriques

Basculez dans le volet de géométrie en utilisant le bouton. Dans le menu du volet de géométrie choisissez Objets puis Point et enfin Point Repéré (Objets / Point / Point Repéré).

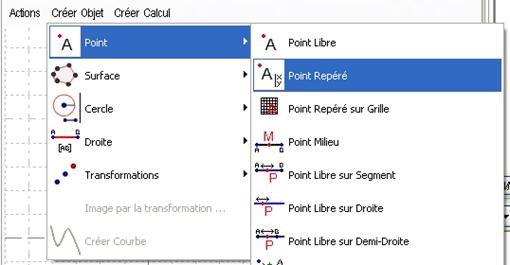
Figure 20 : Menu Créer Objet / Point / Point Repéré

Une boite de dialogue s'ouvre, pour x indiquez 0 et pour y, a. Cliquez sur Créer puis Sortir.

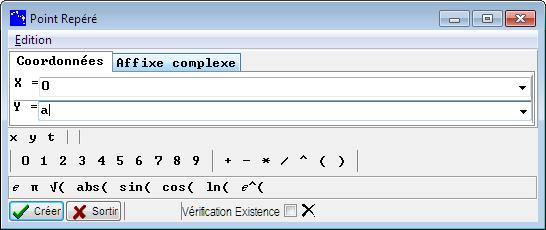
Figure 21 : Boite de création de point repéré

Eventuellement, animez le paramètre pour que le point soit visible.

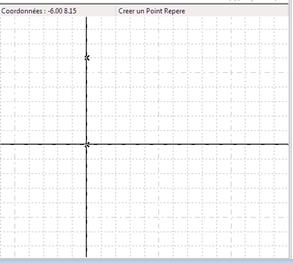
Figure 22 : Premier point dans le volet de géométrie

En sélectionnant le point et en utilisant le clic droit (menu contextuel), vous pouvez renommer le point. Appelez-le B. Renommez aussi l’origine en O.

Avec le même menu contextuel, vous pouvez accéder aux propriétés du point, par exemple la position de son étiquette (Label). Voyez aussi la définition algébrique de l’objet (ici un couple de coordonnées).
             

Figure 23 : Menu contextuel des points et Propriétés                                             Figure 24 : Points renommés B et O

Nous allons créer 2 cercles : Créer Objet / Cercle / Cercle par Centre et passant par un Point. Le premier cercle est de centre O et passe par le point B, le second est de centre B et passe par O. Vous pouvez aussi utiliser le bouton . Note : le fonctionnement des boutons de géométrie est le même que dans d’autres logiciels comme GeoGebra. Vous pouvez vous faire aider par quelqu’un qui connait un de ces logiciels.
             

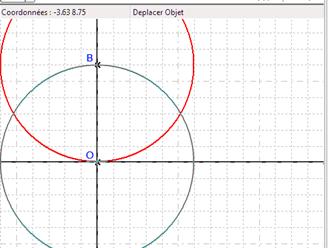
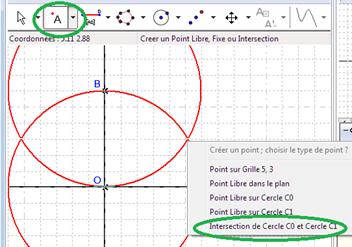
Figure 25 : Les cercles                                                                                                     Figure 26 : Créer un point d’intersection

Nous allons créer un des points d'intersection des 2 cercles : Objet / Point libre ou Intersection ou utilisez le bouton{C}{C}{C}{C}{C}{C}{C}{C} . Pointez sur une des deux intersections et choisissez le dernier item du menu proposé. Renommez le point créé en C. Il est possible de cacher les cercles, les axes (menus contextuels) et la grille (menu action), de créer le triangle OBC (bouton ) et de repositionner les étiquettes des points.

Note : il aurait été possible de créer le troisième point du triangle « à la volée », en actionnant le bouton  puis en cliquant successivement sur les points O et B et sur le point d’intersection à créer.

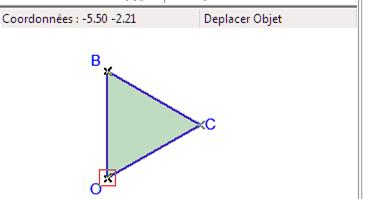
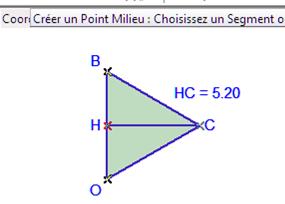
Figure 27 : Le triangle                                                                                                          Figure 28 : Point milieu H et segment HC

Créons le point H milieu de [oB] : Objets / Point / Milieu ou bouton dans la liste du bouton  . Sélectionnez le segment [oB], ou successivement O et B. Nommez le point H. Créez le segment CH (Objets / Droite / Segment ou bouton ). Le menu contextuel du segment propose une entrée Afficher Longueur. Ceci provoque la création d’une étiquette qu’il est possible de repositionner relativement au segment. La valeur approchée affichée est calculée avec la valeur actuelle du paramètre a.

Nous allons maintenant rechercher une expression mathématique de cette distance, qui est la hauteur d’un triangle équilatéral de côté a. Passez dans le volet de calculs géométriques (bouton).

Créons le calcul CH. Cliquez sur Créer Calcul. Dans la boite qui s'ouvre, renseignez la case Calcul avec CH. Cliquez sur Créer.

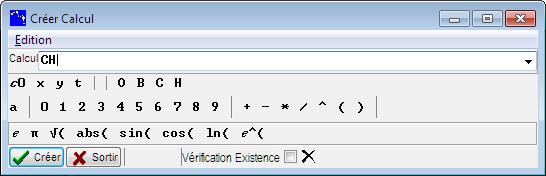
Figure 29 : Création du calcul géométrique CH

Dans le volet calculs géométriques, Casyopée a créé le calcul c0. Si vous préférez avoir c0  sous la forme d(C,H), choisissez dans menu général Options / Volets algèbres / Affichage Distance d(,).

Lorsque le calcul est coché, on observe une valeur approchée cohérente avec l’étiquette affichée sur la figure. Comment dépend-t-elle du paramètre a ? Dans la barre d'outils, faites varier la valeur de a avec le curseur. Observez les changements dans la figure ainsi que le résultat du calcul c0. La valeur de CH dépendrait du paramètre a. Pour vérifier cette hypothèse, mettez en surbrillance le calcul c0 en cliquant dessus, et dans le menu contextuel (click droit) choisissez Dépendance.

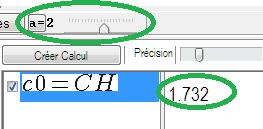
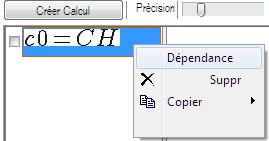
Figure 30 : Le volet Calculs géométriques

Une boite s'ouvre, elle indique que le calcul ne dépend d'aucun point libre et donne une expression algébrique. Elle propose de l'exporter comme expression. Choisissez OK.

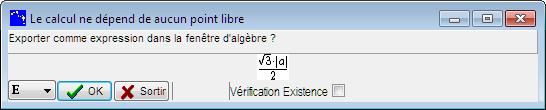
Figure 31 : Boite d'exportation  de calcul

En repassant dans le volet d’algèbre (grâce au bouton ), dans la liste des expressions observez la nouvelle expression E, dont la  formule permet de connaître la valeur de la hauteur d'un triangle équilatéral de coté a.

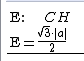
Figure 32 : Expression de la hauteur d'un triangle équilatéral de coté a