Suite définie par un algorithme
Suites dans le volet de géométrie
Une suite de nombres réels (suite numérique) est une fonction de IN vers IR.
La variable est appelée "indice". Dans Casyopée l'indice des suites est la lettre n .
Pour définir des suites, il convient de choisir cette lettre dans la liste en haut à gauche du volet d'algèbre.
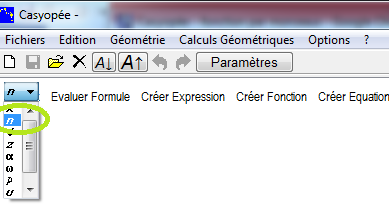
Dans le menu de la fenêtre d'algèbre, l'entrée Créer Fonction est remplacée par Créer Suite.
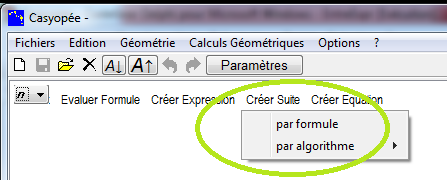
Il y a deux façons de créer une suite.
Suite définie par une formule
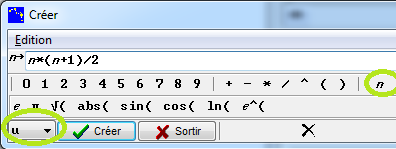
Ce choix correspond à une définition explicite. La boîte d'entrée s'ouvre.
L'identificateur (le nom) de la suite est une lettre à choisir dans la liste en bas à gauche.
L'indice n est entré au clavier ou par le bouton à droite.
La syntaxe est celle des formules de Casyopée.
Après la création, la suite s'affiche avec sa définition dans la liste des expressions.
Les boutons en bas du volet graphique permettent d'obtenir un tracé graphique et la limite.
Sur le tracé graphique, la trace permet d'obtenir les valeurs de la suite.
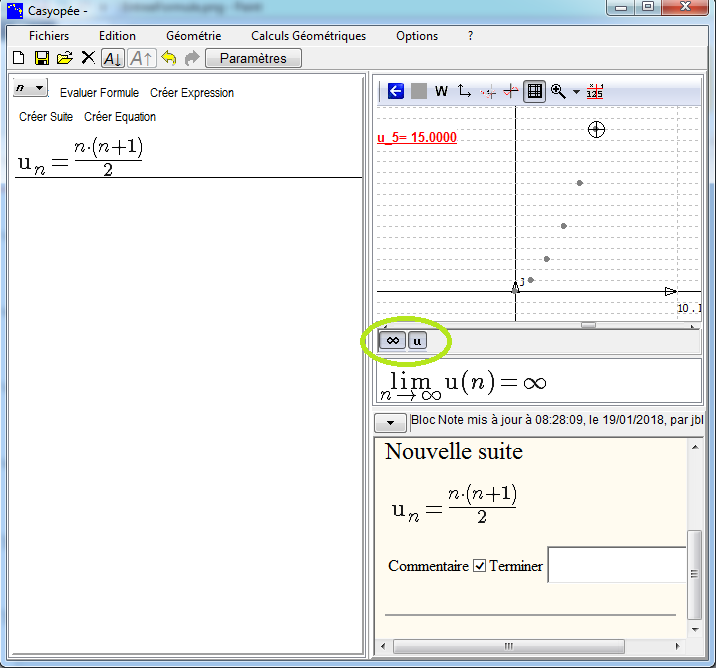
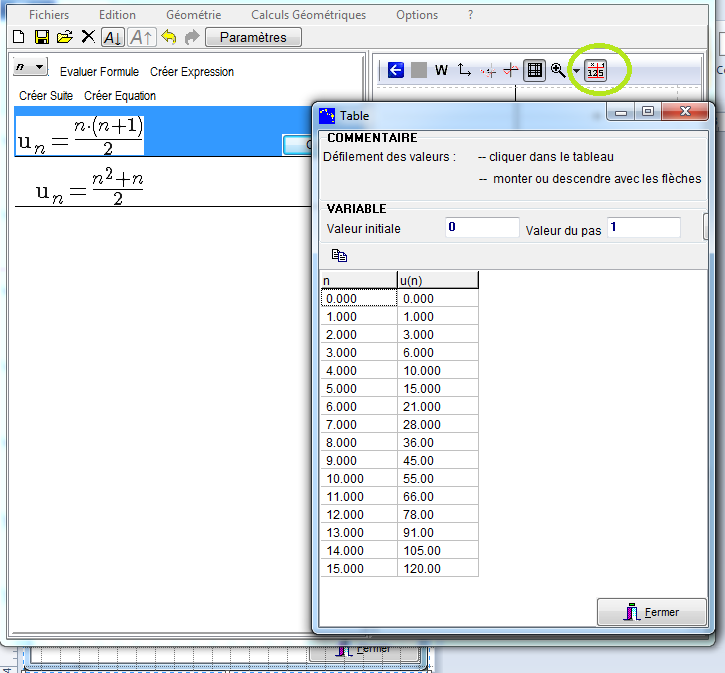
Il est aussi possible d'obtenir une table de valeurs avec un bouton en haut du volet graphique.
La fonction des autres boutons est la même que pour les graphes de fonctions.Voir Calculer, Grapher, Tabuler, Résolution Approchée
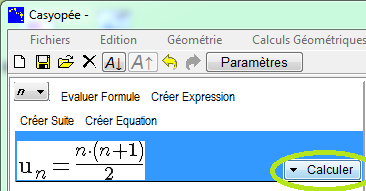
Comme pour les fonctions, le bouton Calculer pemet de réaliser des calculs symboliques.
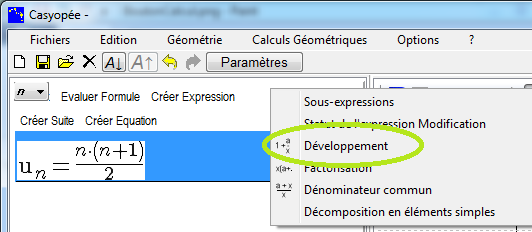
Choisissons par exemple Développement
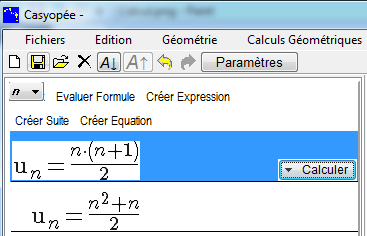
L'expression développée s'affiche dans la liste des expressions
Suite définie par un algorithme
Ce choix correspond à une suite définie par récurrence.
Quand on choisit cette sous-entrée, une liste permet de choisir l'identificateur (le nom) de la suite
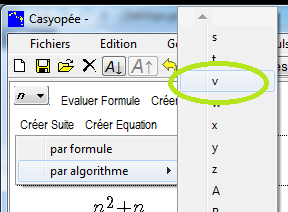
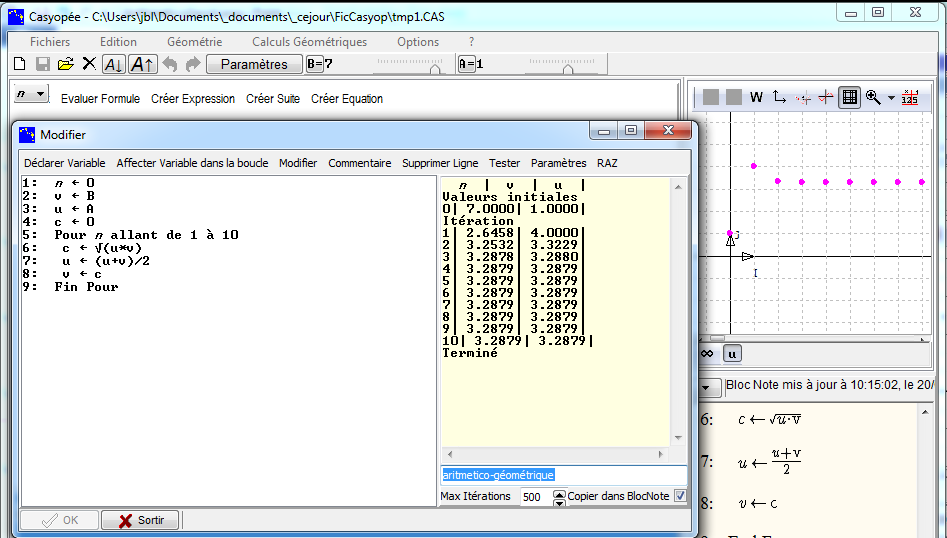
La boîte d'entrée de l'algorithme s'ouvre. Les valeurs initiales de n et de la suite sont données dans les lignes 1 et 2.
Il est possible de modifier la ligne 2 pour une autre valeur initiale.
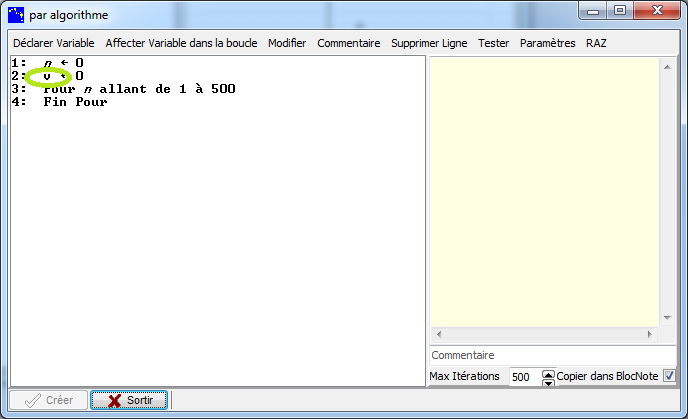
La forme d'itération proposée est la boucle POUR...FINPOUR qui permet de programmer un nombre donné de valeurs.
Nous entrons dans le corps de boucle une formule de récurrence avec Affecter Variable dans la boucle.
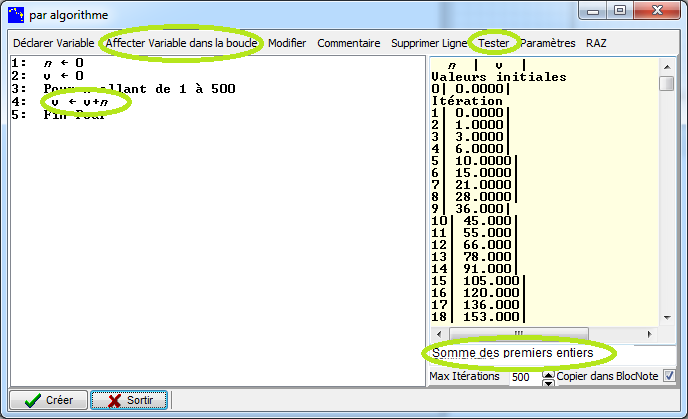
Il faut ensuite Tester avant de cliquer sur le bouton Créer. On peut mettre un commentaire en bas à droite.
Après création, la suite s'affiche avec le commentaire dans la liste des fonctions. Les tracés graphiques de u et v se superposent.
Casyopée ne calcule pas de limite pour v, car, contrairement à u, cette suite n'a pas de définition formelle.
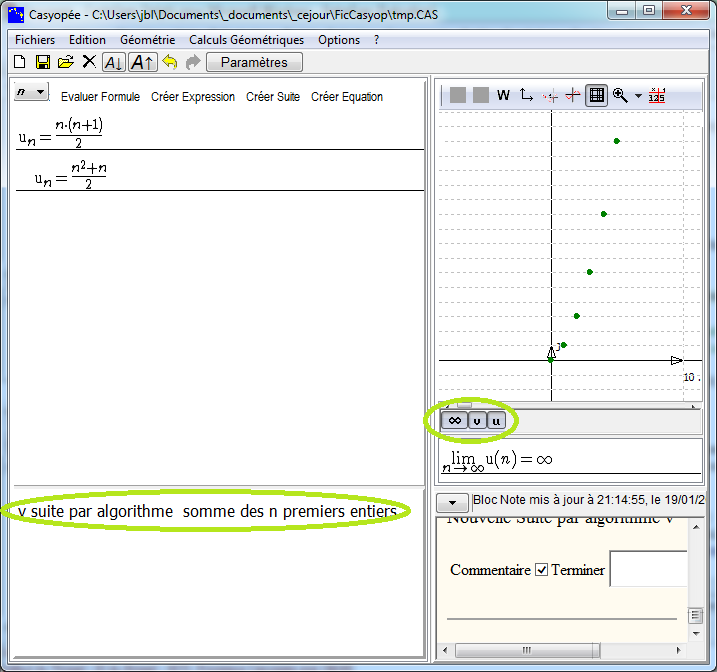
Il est possible de créer des suites avec des algorithmes plus complexes, utilisant des variables globales (paramètres de Casyopée) et locales (entrée Déclarer variable).
Voir la page Fonctions définies par un algorithme.
Ci-dessous, l'exemple d'une suite convergent vers la moyenne arithmético-géométrique de deux nombres A et B.
Suites dans le volet de géométrie
Dans le volet de géométrie, il est possible d'afficher les suites dans le même écran que des courbes de fonction et d'autres objets géométriques. Il est possible aussi de créer un point libre suivant les éléments de la suite. Voir la page Courbe et nombre dérivé.
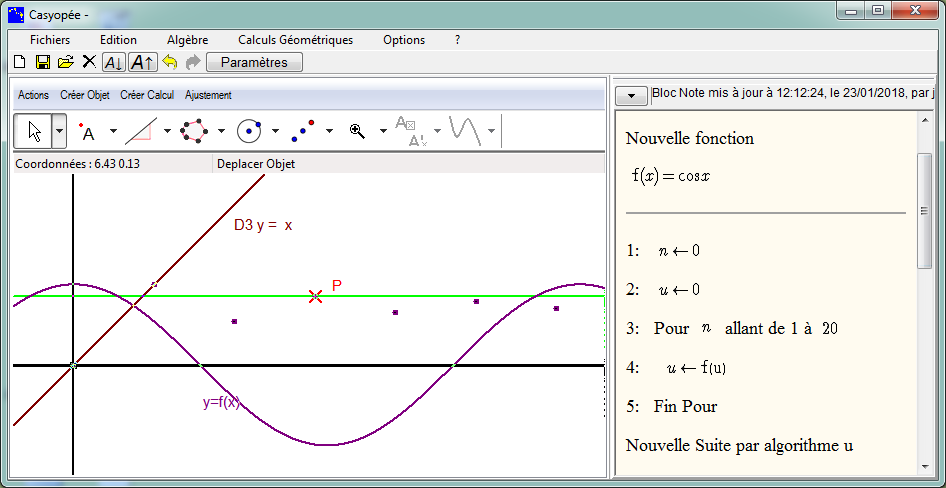
Ci-dessous, on définit par un algorithme une suite u convergeant vers le point fixe de la fonction cosinus. Le point libre P suit les éléments de la suite. A l'aide d'une parallèle à l'axe des x passant par P, et en tirant ce point, on observe que les valeurs de la suite (l'ordonnée du point P) encadrent l'ordonnée du point d'intersection de la représentation de la fonction cosinus et de la première bissectrice.
Catégorie : -
Page lue 10508 fois




