Traduire des conditions aux bornes d’un l’intervalle
On considère trois fonctions f, g et h :
- h est définie sur [- 2 ; 1] par h (x) = ax + b.
- g est définie sur [1 ; + [ par g(x) = (x– 1)² + 3 ;
- f est définie sur ]- ; - 2] par f (x) = - (x + 2)² – 1 ;
Créez les fonctions f , g et h (comme ci-dessus Créer fonction par domaine + formule), contrôlez que les ensembles de définition sont corrects.
Remarque : Dans les boites de dialogue, l'écriture des puissances se fait avec le symbole "^", ainsi pour la fonction f, il faut écrire : -(x + 2)^2 – 1.
Piloter les paramètres
Les paramètres ont été créés avec la fonction h. Par défaut, un curseur est visible (paramètres "dépliés"). Vous pouvez les "plier" pour gagner de la place en cliquant sur l'identificateur.
![]()
![]()
Figure 48 : Paramètres "dépliés" dans la barre d'outils Figure 49 : Paramètre "plié"
Lorsqu'ils sont "dépliés" , vous pouvez les piloter en déplaçant le curseur avec la souris ou avec les flèches du clavier.
Les valeurs prises par les paramètres sont celles de l’intervalle ]minimum ; maximum[ du paramètre.
Visualisez f, g et h dans le volet graphique, le graphe de la fonction h prend en compte les valeurs des paramètres a et b.
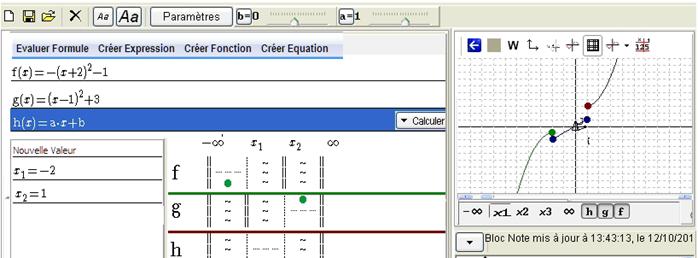
Figure 50 : Visualisation des fonctions f, g et h
Pour modifier le pas du paramètre, qui détermine de combien avance le paramètre à chaque graduation, ouvrez de nouveau la boite des paramètres en cliquant sur le bouton Paramètres, puis inscrivez le nouveau pas dans le cadre correspondant. Notez qu’il est possible d’affecter une vitesse à chaque paramètre. Si cette vitesse n’est pas nulle, le paramètre parcourra automatiquement la plage des valeurs. Ceci permet d’animer un graphe ou une figure géométrique.
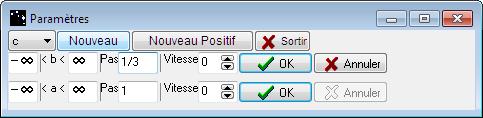
Figure 51 : Changement du pas du paramètre a
Traduire des conditions aux bornes d’un intervalle
Vérifiez que les paramètres sont sous forme formelle.
Dans le volet graphique, sélectionnez les trois fonctions et successivement x1 et x2. Dans la liste des valeurs symboliques apparaissent les conditions algébriques car les paramètres ne sont pas instanciés.
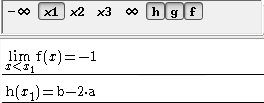
Figure 54 : Limite en x1 en fonction des paramètres a et b
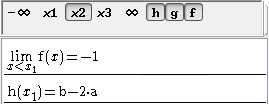
Figure 55 : Limite en x2 en fonction des paramètres a et b
Ces conditions sont b – 2a = -1 et a + b = 3.
En résolvant ce système vous obtenez les valeurs pour a et b (a = et b = ).
Note : Casyopée ne résout pas les systèmes d’équation. La résolution par substitution peut être faite à l’aide d’équations successives. Pour les experts, l’entrée Evaluer une formule dans la barre de menus de la liste des expressions permet la résolution par Maxima (Figure 56). Il est aussi possible d’entrer une commande comme solve([g(x2)=h(x2), g(x1)=f(x1)],[a,b]).
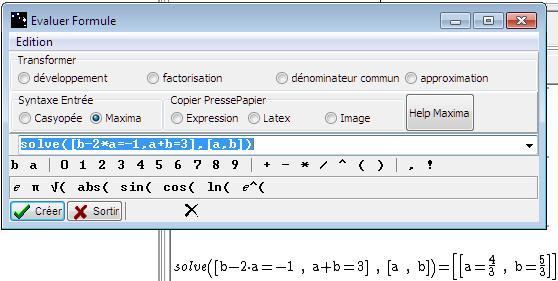
Figure 56 : Un exemple d’utilisation d’une commande Maxima.
Pilotez les paramètres pour leur donner ces valeurs et contrôlez graphiquement. Si le pas ne convient pas, cliquez sur le bouton Paramètres, puis dans la boite mettez 1/3 comme pas.
Instancier des paramètres dans les expressions
Il est possible d'instancier un ou plusieurs paramètres dans une expression grace au menu contextuel (click droit). On coche le ou les paramètre(s) et l'expression s'affiche de façon particulière.
Les valeurs ou limites d'une fontion affichées dans la liste des valeurs symboliques sont instanciées selon les choix faits pour l'expression définissant cette fonction.
Substituer des paramètres
Mettez l’expression de h en surbrillance. Dans le menu déroulant Calculer, choisissez substituer ; les valeurs des paramètres a et b sont remplacées par celles affichées dans les zones de pilotage. Les paramètres doivent être instanciés.
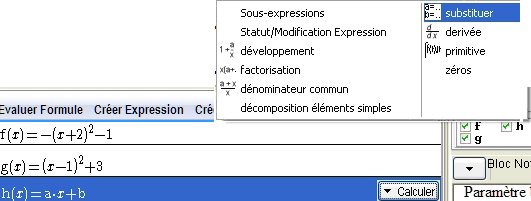
Figure 57 : Substitution des paramètres
Une boite de confirmation s’ouvre. Cliquez sur Confirmer. Une nouvelle fonction notée h0, indépendante de la fonction h, a été ainsi créée.
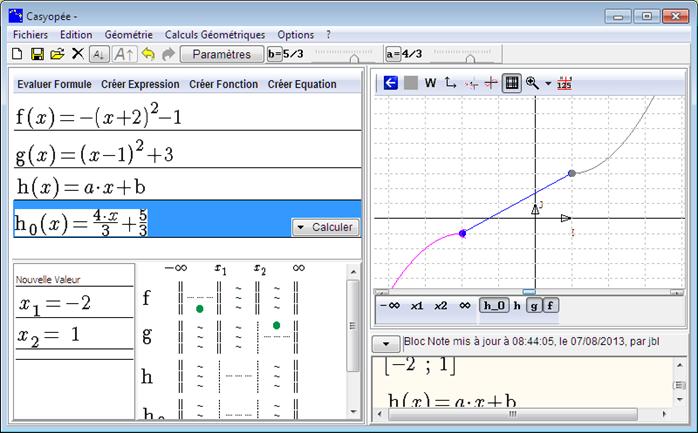
Figure 58 : Visualisation graphique de la substitution
Catégorie : - aide
Page lue 9010 fois




