Déterminer le signe d’une fonction affine
Déterminer les variations d’une fonction affine
Justifier le signe à partir des variations
Déterminer le signe d’un produit
Nous prenons l'exemple d'un produit de fonctions affines.
Deux méthodes pour déterminer le signe d’une expression affine seront utilisées :
- l’une utilise un résultat sur le signe des expressions affines (méthode 1),
- l’autre utilise le sens de variation d’une fonction affine (méthode 2).
La conclusion utilise la règle des signes pour un produit ou un quotient.
Trouver des sous-expressions
Entrez la fonction f (il est important de cocher Vérification Existence).
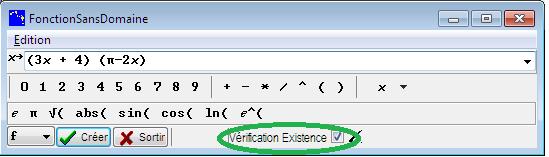
Figure 62 : entrée fonction sans domaine
Dans la liste des expressions, cliquez sur l’expression de f. Cliquez sur le bouton Calculer, dans le menu contextuel qui apparaît choisissez Sous-expressions. Une boite apparaît avec la liste des sous expressions
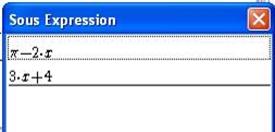
Figure 63 : Liste des sous-expressions
La sélection dans la liste des sous expressions s’effectue comme dans une fenêtre de WindowsTM explorer : En restant appuyé sur « ctrl » cliquez ou non sur les sous expressions
En restant appuyé sur « Shift » ou sur , cliquez sur la première expression puis sur la dernière que vous voulez sélectionner ; le bouton Tout permet de les sélectionner toutes.
Dans cet exemple choisissez Tout, puis validez avec OK. La liste des expressions et celle des fonctions sont ainsi complétées et les nouvelles expressions (respectivement fonctions) sont nommées f0 et f1.
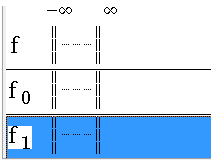
Figure 64 : Sous-expressions (listes des fonctions) Figure 65 : Sous-expressions (listes des expressions)
Si la fenêtre des fonctions n’est pas visible, faites la apparaître avec Options Fenêtres.
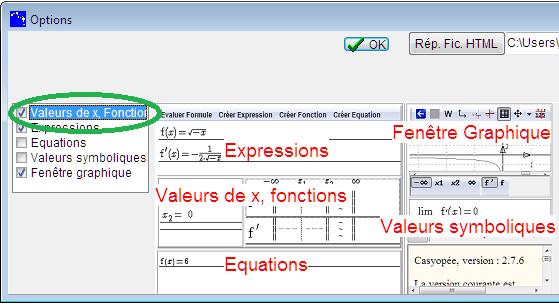
Figure 66 : menu Options Fenêtres
Déterminer le signe d’une fonction affine
Dans la liste des fonctions, mettez en surbrillance f1 comme ci-dessus. Dans le menu Justifier choisissez Signe : affine. Une boîte de dialogue apparaît :
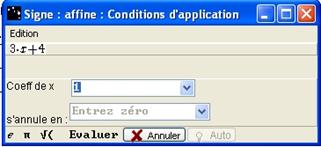
Figure 67 : Boîte "Signe : affine"
Renseignez le Coeff. de x (coefficient directeur) et s’annule en (le zéro) puis, cliquez sur le bouton Evaluer.
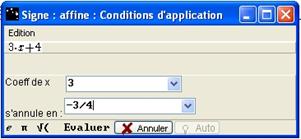
Figure 68 : Boîte "Signe : affine" renseignée avec des erreurs
S’i l y a une erreur, une information s’affiche dans le Bloc Note :
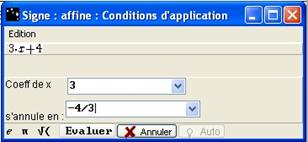
Figure 69 : Boîte "Signe : affine" renseignée correctement
Si les valeurs entrées sont correctes, après avoir cliqué sur Evaluer une nouvelle boite s’affiche :
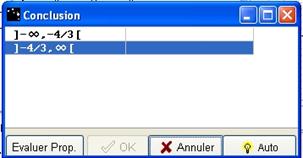
Figure 70 : Boîte "conclusion" signe
Pour chaque ligne cliquez sur la case vide jusqu'à obtenir négative ou positive. Evaluez vos propositions en cliquant sur Evaluer Prop.
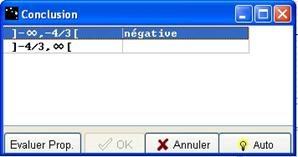
Figure 71 : Boîte "conclusion" 1ere ligne renseignée
Quand vos propositions sont correctes le bouton OK est activé ; cliquez dessus.
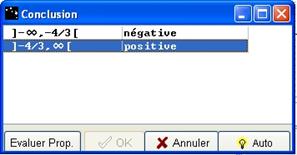
Figure 72 : Boîte "Conclusion" renseignée
Le zéro de f1 est mis dans liste des Valeurs de x et le signe de f1 est mis sous forme de ronds verts (positif quand le rond est au dessus de la ligne horizontale passant par 0, négatif sinon).
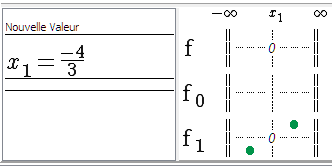
Figure 73 : Visualisation signe dans la liste des fonctions
Déterminer les variations d’une fonction affine
Pour déterminer le signe de (π – 2x) créez d’abord le zéro de la fonction f0 (c’est-à dire π/2) dans la liste des Valeurs de x (avec le bouton Nouvelle Valeur), puis sélectionnez f0 dans la liste des fonctions.
Dans le menu Justifier choisir Variations : fonction de référence.
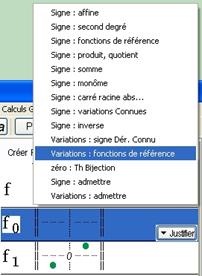
Figure 74 : Menu Justification Variation
Cette boite s’ouvre :
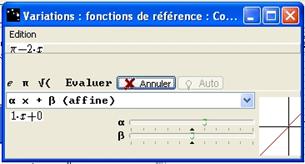
Figure 75 : Boîte "Variations"
Vous pouvez choisir le type de fonction dans la liste et vous obtenez une représentation graphique de la fonction sélectionnée. Cliquez sur le bouton Evaluer. Si le choix est correct une boite de Conclusion s’ouvre :
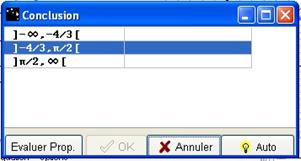
Figure 76 : Boite "Conclusion" variations
Pour chaque ligne, cliquez sur la case vide pour faire apparaître croissante ou décroissante.
Evaluez vos propositions en cliquant sur Evaluer Prop.
Quand vos propositions sont correctes le bouton OK est activé ; cliquez dessus.
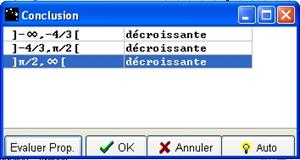
Figure 77 : Boîte "Conclusion" variation renseignée
Le sens de variation de f0 se traduit par des flèches dans la liste des fonctions.
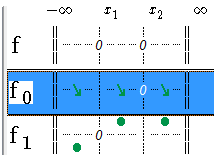
Figure 78 : Visualisation des variations
Justifier le signe à partir des variations
Après avoir déterminé le sens de variation il faut justifier le signe. Dans le menu Justifier choisissez Signe : variations Connues.
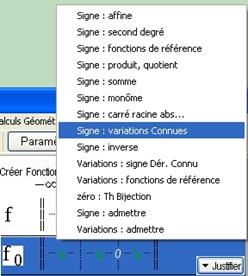
Figure 79 : Menu signe-variation connues
La boite Signe : variations Connues : Conditions d'application s'ouvre. Indiquez pour l'une des valeurs du menu déroulant si la fonction est négative, nulle ou positive. Ici, indiquez x2 et choisissez fonction nulle. Le bouton Evaluer devient accessible, cliquez dessus.
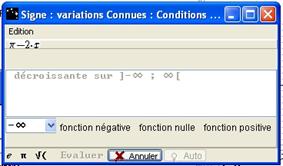
Figure 80 : Boite "Signe : variations Connues"
Une boite de Conclusion apparaît. Pour chaque ligne, cliquez sur la case vide jusqu'à obtenir positive ou négative. Evaluez vos propositions en cliquant sur Evaluer Prop. Quand vos propositions sont correctes, le bouton OK est activé ; cliquez dessus.
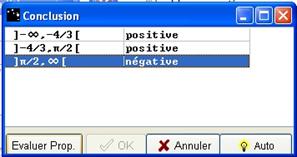
Figure 81 : Boite "Signe : variations Connues" renseignée
Le signe de f0 est indiqué dans la liste des fonctions par la position des flèches vertes. Au-dessus de la ligne de pointillés passant par zéro, la fonction est positive et en dessous, la fonction est négative.
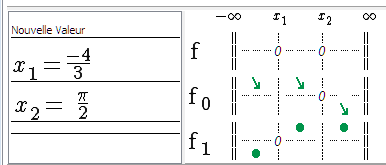
Figure 82 : Visualisation du signe de f0
Déterminer le signe d’un produit
Enfin sélectionnez f et choisissez dans le menu Justifier, Signe : produit, quotient.
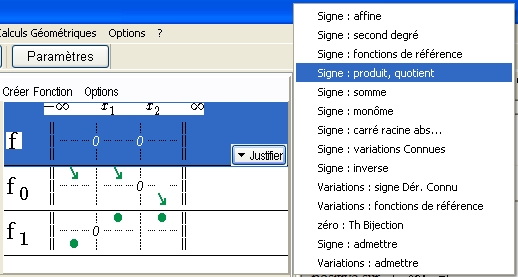
Figure 83 : Menu Justifier / Signe : Produit, quotient
En bas de la boite de dialogue, sélectionnez les deux lignes car f est le produit de f0 et de f1.
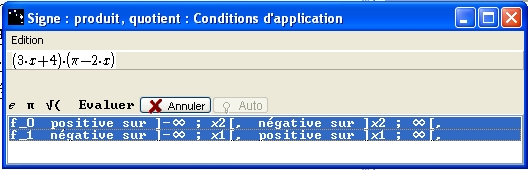
Figure 84 : Boîte "Signe : produit, quotient"
Cliquez sur Evaluer pour obtenir la boite ci-dessous dont le fonctionnement a déjà été expliqué.
Cliquez sur Evaluer Prop. puis sur OK. Le signe de f apparaît dans la liste des fonctions.
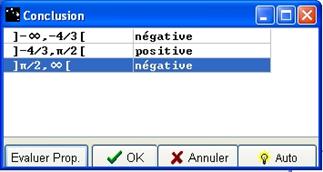
Figure 85 : Conclusion signe
Au final, le tableau de signe dans la liste des fonctions est complètement rempli. Le contenu du Bloc Note permet de se rappeler toutes les étapes et constitue une base pour la rédaction d'une justification. Il est en effet possible d’afficher la source, de l’éditer avec quelques commandes simples et de le sauvegarder sous forme de fichier MIME HTML, d’extension mht que beaucoup d’explorateurs et de traitements de texte peuvent ouvrir.
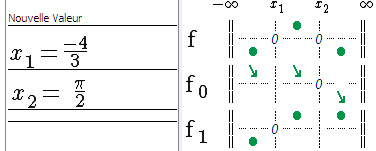
Figure 86 : Tableau de signe des fonctions
Catégorie : - aide
Page lue 10917 fois
Prévisualiser...
Imprimer...
