Construction
Modélisation
Animation
Nous étudions la dépendance entre un calcul géométrique et une variable géométrique en traitant un exemple d’optimisation d’une aire.
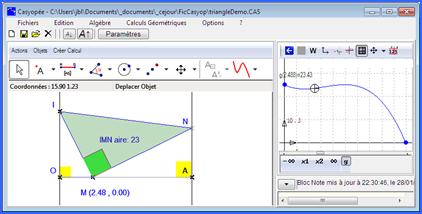
Un segment [OA] de longueur 10, un point M mobile sur ce segment, un point I sur la perpendiculaire en O à (OA), N le point sur la perpendiculaire en A à (OA) construit de façon que le triangle MIN soit rectangle en M. On cherche la (les) position(s) de M maximisant l’aire du triangle.
Construction
|
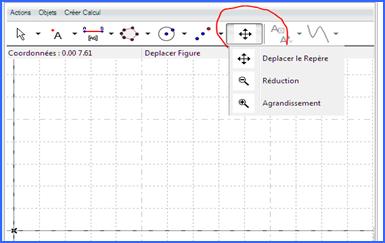
Nous nous plaçons dans le cas OI=5 Le fonctionnement des boutons de construction est similaire à celui de GeoGebra. Chaque bouton donne accès à un ensemble de fonctions. On commencera par adapter l’écran de géométrie avec le bouton servant à déplacer et à zoomer. |
Figure 87 : Zoom et déplacement |
|
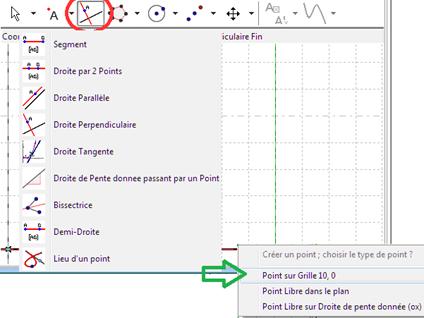
Ensuite, on crée une droite perpendiculaire à l’axe des x au point de coordonnées (0, 10), puis le segment de l’origine à ce point. Création de segment et de perpendiculaire sont sous le même bouton. Cliquez d’abord sur l’axe des x, puis à proximité du point de coordonnées (0, 10). Choisissez dans le menu comme indiqué sur la figure. |
Figure 88 : Création droite perpendiculaire |
|
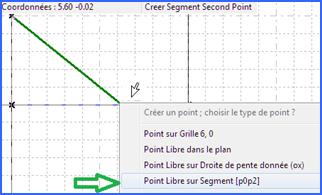
On crée de même un segment du point de coordonnées (5,0) vers un point libre sur le segment qui vient d’être créé. Attention, il faut bien choisir le point dans le menu. |
Figure 89 : Création segment |
|
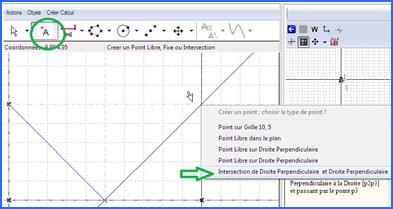
On créée ensuite la perpendiculaire au segment passant par le point libre. Le bouton point permet de choisir le point d’intersection voulu par un menu quand la souris est proche de cette intersection. |
Figure 90: création perpendiculaire vers un point libre |
|
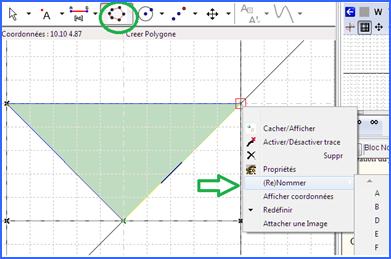
Le bouton polygone permet de créer un triangle en cliquant successivement sur chaque point. Il est temps de donner un nom aux points Ceci se fait en utilisant le menu contextuel (clic droit) de chaque objet. |
Figure 91 : Création triangle et nommage des points |
|
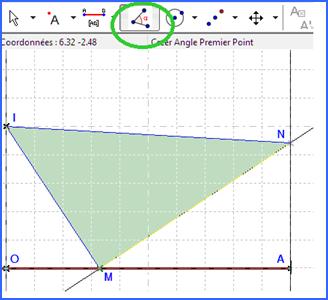
On peut aussi créer des angles avec le même bouton que les polygones : on clique successivement trois points. |
Figure 92: Création angles |
|
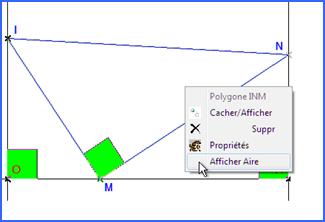
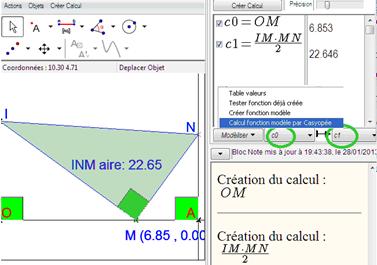
Ici, les angles choisis sont codés comme des angles droits. On peut faire afficher certains éléments (aire, coordonnées) toujours en utilisant le menu contextuel. |
Figure 93: création d'une étiquette (aire) |
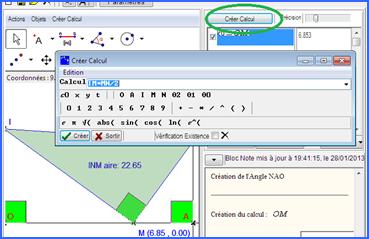
ModélisationNous allons passer à la modélisation. Basculez dans le volet de calculs géométriques (bouton Nous devons créer des « calculs géométriques » pour la variable et la valeur de la fonction. Cliquez sur |
Figure 94 : calcul géométrique |
|
Casyopée leur donne les étiquettes c0 et c1. Choisissons c0 et c1 dans les listes à droite du bouton modéliser. |
Figure 95 : modélisation |
|
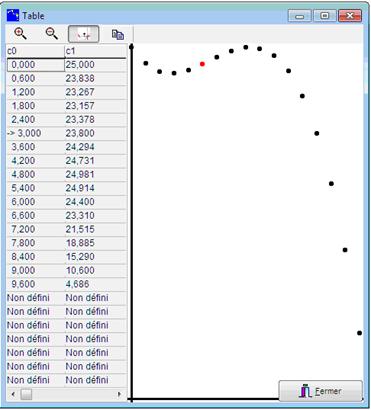
Le bouton « modéliser » donne accès à un menu où nous choisissons l’entrée : Table Valeurs Les valeurs prises par les deux calculs pour une série de positions du point M s’affichent. Le bouton La visualisation graphique permet de conjecturer une dépendance fonctionnelle de c0 à c1. Nous allons modéliser algébriquement cette dépendance. |
Figure 96 : modéliser, table valeurs |
|
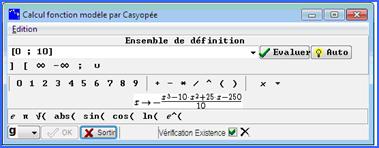
Le bouton « modéliser » donne accès à un menu où nous choisissons l’entrée : calcul fonction modèle par Casyopée. L’ensemble de définition et une formule pour la fonction sont calculés par Casyopée. Il est important de cocher la case Vérification Existence. |
Figure 97 : modéliser calcul fonction modèle par Casyopée. |
|
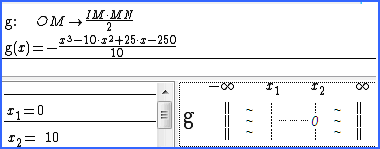
Après acceptation des données, la fonction est créée dans le volet Algèbre. Le mini tableau s’affiche car le domaine a été vérifié à l’étape précédente. Il est alors très simple de prouver par une étude de variation aidée par Casyopée, des conjectures émises par observation sur la figure |
Figure 98 : fonction modèle On conjecture puis on prouve deux maximas, l’un quand M est en 0, l’autre quand il est au milieu de [OA]. |
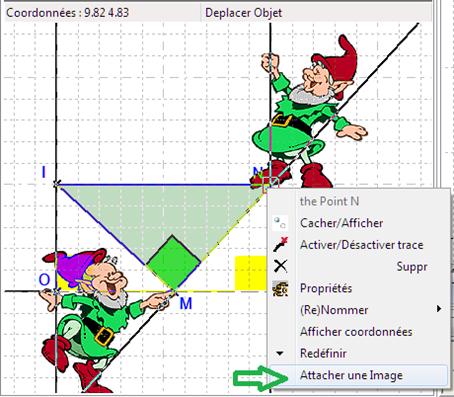
AnimationRevenez au volet de géométrie (entrée de menu Vous pouvez Attacher une image à des points (ici M et N). Une fois attachées, ces images pourront être déplacées relativement aux points. Pour créer une animation, donner une vitesse au point M (menu contextuel, Propriétés) et enregistrer l’écran en GIF animé (menu Fichiers). |
Figure 99 : insertion d'images et animation |
Catégorie : - aide
Page lue 8942 fois