Casyopée - Angle et Modélisation

Le site sera traduit dans la langue secondaire: en

Ils l'ont dit : J'ai traité des exercices d'optimisation avec Casyopée. Il permet pour ce type de recherche une disparition presque complète de l'énoncé, l'élève arrivant à des résultats qu'il démontrera ultérieurement. Le logiciel permet de plus de réinvestir des stratégies de base. Un enseignant

Ils l'ont dit : Casyopée est plus rapide et plus commode qu'une calculatrice…. On a en même temps le côté géométrique et algébrique du problème. On voit mieux comment une fonction « réagit ». C’est pratique et intéressant. Une élève

Ils l'ont dit : Casyopée permet de faire les calculs facilement d’une dérivée, de factoriser, de calculer les zéros… et d’avoir à côté dans la même fenêtre un graphique de la fonction. Il permet sur un problème géométrique de pouvoir établir des variables qui pourront ensuite servir pour étudier le problème par des fonctions… Une élève

Ils l'ont dit : Casyopee est une application puissante utile à la fois pour les étudiants et les enseignants Il vous permet d'utiliser divers outils d'exploration et de modélisation, dans le but d'étudier ou d'enseigner des fonctions mathématiques. Softpedia

Ils l'ont dit : Casyopee a beaucoup de fonctionnalités. Il existe une aide pour prouver les propriétés d'une fonction et une fonctionnalité pour l'écriture de rapports HTML qui comprennent les fonctions mathématiques. Casyopee garantit les progrès en mathématiques de ses utilisateurs. phpnuke.org

Ils l'ont dit : Hormis les nombres, la notion de fonction est la plus importante en mathématiques. David Hilbert

Ils l'ont dit : La notion de fonction est présente dans toutes les disciplines scientifiques, mais aussi dans la vie courante. Notre expérience d’enseignants nous prouve quotidiennement qu’il pose problème pour de nombreux élèves. Les situations avec Casyopée sont également utilisables en dehors d’un environnement technologique et chacun pourra réfléchir sur sa pratique professionnelle. Une universitaire

Angle et Modélisation

Bielle et vilebrequin

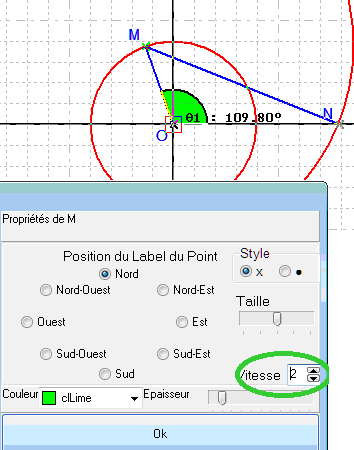
Soit M un point mobile sur le cercle de centre O et de rayon 1. Soit N le point de l’axe des x à distance a de M, a étant un paramètre positif. On s’intéresse à la distance ON en fonction de la position de M. Pour les mécaniciens, le segment [OM] est partie du vilebrequin, et le segment [MN] représente la bielle. On s’intéresse à la distance ON, c’est-à-dire la, distance entre l’axe du vilebrequin et le piston, en fonction de la position de M. On repère cette position par la valeur de l’angle entre l’axe des x et le rayon [OM].

Figure 100 : la bielle, construction et animation

Point p0 renommé en O

Création du cercle C1 de centre O et de rayon 1.

Création du point libre p1 sur le cercle C1 renommé en M.

Paramètre a positif.

Création du cercle C2 de centre M et de rayon a.

Création du Point p2 à l’intersection de C2 et (Ox) renommé en N.

Création du Point Repéré p3 (3,0)

Création de l'Angle p3OM : Theta1.

Vous pouvez affecter une vitesse au point M pour voir le mécanisme s’animer.

Le calcul géométrique à choisir pour la valeur de la fonction est ON. Celui à choisir pour la variable est q1.

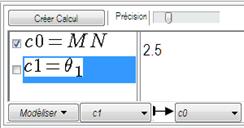
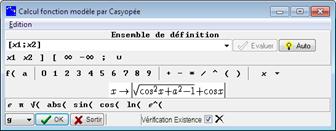
Figure 101 : la bielle, modélisation

Après avoir fait calculer la fonction modèle et avoir validé l’ensemble de définition et la formule donnée par Casyopée, on obtient un message d’avertissement indiquant que Maxima ne peut certifier l’existence de cette fonction.

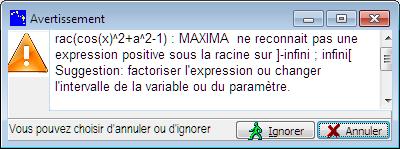
Figure 102 : Avertissement de Maxima

Notez qu’un tel avertissement peut se produire alors que la définition est correcte mathématiquement, du fait des limites du calcul formel. C’est pourquoi la possibilité vous est laissée d’ignorer l’avertissement après une nouvelle mise en garde : la fonction pourra être créée. Fin de cet exemple.

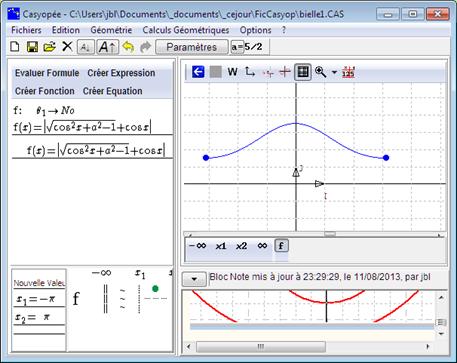
Figure 103 : la bielle, fonction modèle

Date de création : 06/10/2014 - 16h14
Catégorie : - aide
Page lue 8800 fois