Paramètres géométriques dans les fonctions
Dans Casyopée, les fonctions font le lien entre la géométrie et l’algèbre. Ainsi, une fonction peut
1. modéliser une dépendance entre grandeurs géométrique (une unité étant choisie, elle fait passer d’une valeur de la première grandeur à la valeur correspondante de la seconde).
2. être la fonction dont une droite donnée est la représentation graphique (modélisation d’une droite).
3. être la fonction dont le lieu d’un point est la représentation graphique (modélisation d’un lieu).
1. Un exemple de modélisation de dépendance avec « le triangle de Minh »
|
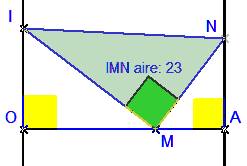
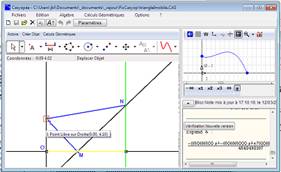
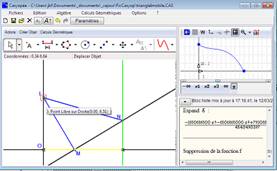
A sur l’axe des x, O origine du repère, I sur l’axe des y, OA=10, OI=5, M est un point libre sur [OA] et IMN est rectangle en M. Il s’agit d’étudier les variations de l’aire du triangle MIN. Une fonction modèle est Supposons maintenant que l’on veuille étudier les variations pour une position quelconque du point I sur la droite. On redéfinit I comme point libre sur l’axe des y. La fonction modèle depend alors de la position du point I
En tirant le Point I dans le volet Géométrie, on observe la déformation continue du graphe de la fonction modèle. En fait, la formule de la fonction modèle depend d'un parameter géométrique tI, représentant la position de I sur l’axe des y. Il est possible de faire afficher ce parameter par le menu Options-Calcul et Justification- Instancier les paramètres géométriques.
Il est alors possible d'instancier explicitement les paramètres géométriques.:
|
|
2. "Equations" de droite
|
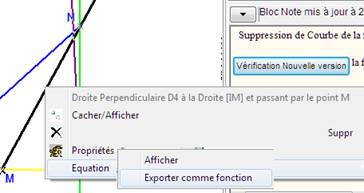
Le menu contextuel des droites donne accès à un menu Equation-Exporter comme fonction. La fonction affine obtenue a pour représentation graphique la droite. Ici la droite dépend des deux points libres I et M, et donc leurs paramètres sont dans la formule.
Notez que par défaut les paramètres géométriques sont instanciés automatiquement. |
|
3. Lieux géométriques
|
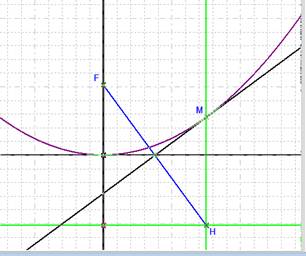
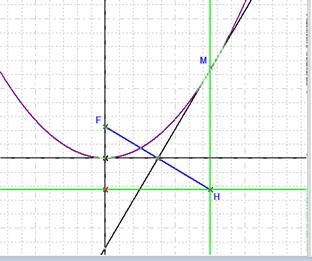
Dans les versions précédentes, il était possible d’obtenir le lieu d’un point seulement si celui-ci ne dépendait que d’un seul paramètre de point libre (par exemple le paramètre d’un point libre sur objet). Exemple : construction d’une parabole par foyer et directrice Création du Point Libre p1 sur (oy) renommé en F Création du point p2 image du point F par la Symétrie de centre p0 Création de la Droite Parallèle D2 à la Droite (ox) et passant par le point p2 Création du Point Libre p3 sur D2 renommé en H Création de la Droite Parallèle D3 à la Droite (oy) et passant par le point H Création du Point Milieu p4 du Segment [FH] Création du Segment [FH] Création de la Droite Perpendiculaire D4 à la Droite [FH] et passant par le point p4 Création du Point d'intersection des droites D4 et D3, p5 renommé en M Avec le bouton En tirant le point F, on change l’excentricité de la parabole. Notez que par défaut les paramètres géométriques sont instanciés automatiquement. |
|
dans le menu des droites,
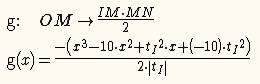
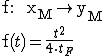est créée et la parabole s’affiche.
Catégorie : - aide
Page lue 8085 fois
