Casyopee functions are real function defined on R on a union of intervals.

The values can be in R or in R². In this latter case, two formulas must be entered, between square brackets and separated by "," or ";".

They are defined by a set of definition and a possibly parametric formula.

Optionnally, Casyopee can check that the formula is valid on the set of definition.

The zero, other formulas (factorized, developed...), the derivative and primitive functions are obtained by calculation.

It is possible to prove properties of sign and monotonicity of functions, whose validity has been checked by Casyopee, by justification.

An exploration can be done by the list of exact values or numerically.

Alternatively, Casyopee allows to define a function by an algorithm. See documentation here

These functions are displayed in the function list, that appears optionally together with the list of  values of the variable

Graphs of the functions can be obtained in the Graphic Tab. See onlinehelp.

Curves of the functions can be obtained in the Dynamic Geometry Tab. 

From several functions defined on disjoint intervals, one can create a piecewise function.

A piecewise function can only be graphed and appear in the list of exact values. No calculation is possible.

The identifier is formed from the identifiers of existing functions (f ∨ g ∨ h…). See onlinehelp.

The sets of definition (or domain) of a function is an interval or of union of intervals.

The bounds of these intervals are chosen in the list of variable values which is already created.

The expressions of Casyopee are defined by formulae which can include parameters, but no variable identifier.

Other expressions (factorized, developed..) are are obtained by calculation..

Formulae are used to create functions, expressions, equations, as well as specific geometrical objects and geometrical calculations. A formula can also be evaluated and transformed, via the Evaluate formula entry of the algebra menu.

The formulae are written with mathematical symbols. Multiplication is implicit. 

Formulae can contain parameters (a, b, c, t, z...) and identifiers of already defined functions and expressions. 

Geometrical formulae

Formulae defining geometrical objects and geometrical calculations can also contain identifiers of named points, for instance to refer to a distance or a coordinate, or special identifiers of angles.

The sub-expressions are factors of a product or of a quotient, or terms are extracted from a sum, or arguments of functions or of expressions.

Casyopee defines then a new function on the same set of definition or a new expression.

It is possible to prove properties of a function from the properties of functions defined by sub-expressions. See onlinehelp.

These are real values which take part in the study as bounds of intervals when defining a function. They can be created by the Casyopee (zeros of functions, symbolic zeros obtained by applying the theorem of bijection) or by the user. The expression of a value can include parameters. In order to keep an ordered list, when creating a value, Casyopee tries to compare this new value with the existing ones first by symbolic methods, otherwise by numerical approximation using current values of parameters.

It is possible to choose the symbol denoting the variable of a function (x, t, α, ...). For each symbol, there is a list of ordered values. The choice of the symbol determines the displayed functions in the list which might be graphed and displayed in the table of exacts values.

The  values are identified under the form xi, i being the number in the increasing values and x being the symbol of the current variable. This identifier can be used in dialog boxes and in the table of properties of functions. 

Values can be traced in the graphic tab as vertical lines. Exact values of functions graphed in the graphic tab appear in the list under this tab.

Casyopee gives exact or approximate solutions of an equation with one unknown. These solutions are displayed in the notepad.

The equations can be of four different natures:

The constant K can depend on parameters but not on the variable.

The unknown can be the variable or a parameter in the fourth case. The domain of resolution is the set of definition of the function in the first case, the intersection of sets of definitions of two functions in the second and the third case, and the interval of variation of the parameters in the fourth case.

In case where the equation comprises only one symbol (numerical equation), Casyopee proposes the exact or approximate resolution.

See Online Help.

A parameter is defined as element of a open interval which can be bounded or not. This property is taken into account in calculations by Casyopee.

The parameters can be used in any formula to define a function, an equation, an expression, a variable value, or a geometrical object, or a geometrical calculation. They can be the unknown of an equation.

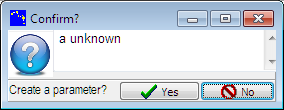
Parameters can be created with the bouton   in the main toolbar. The same button gives access to the list of  parameters and their properties.
The creation of a parameter is proposed when a formula is entered, which includes a letter not already assigned to an object. For instance in the example above after entering an expression, the letter a being not already used, a box asks to confirm the creation of a new parameter.

A parameter has a value, integer or fractional. This value is assigned at random after creating the parameter, or changing the properties. Then it can be assigned by the user via a cursor. A velocity can also be assigned in order to create animations, the parameter taking successive values in the interval. A contextual menu gives access to the properties (bounds of the interval, step of the cursor, velocity).

The value of a parameter is taken in account dynamically in all graphs in the graphic tab, as well as in the display of geometrical objects depending of the parameter, and in approximate values of geometrical calculations.

In contrast, in calculations, symbolic values of functions and equation solving, Casyopee considers parameters as a symbolic entity. Thus parameters are not instanciated in the algebra tab displays (list of expressions, values of the variable) and in the list of symbolic values of functions.
.
It is possible to instanciate an expression by the contextual menu. By checking one or more parameters, the expression is displayed with the actual values. Values or limits of a function displaid in the list of  symbolic values are instanciated  for the parameters instanciated in the initial expression of the function. When parameters have been instanciated in an expression, it is possible to create a new function or expression by substituing the instanciated parameters, thanks to the 'ad hoc' calculation. See onlinehelp.

Geometrical parameters

After modelling a dependency in the geometrical calculation tab, Casyopee may introduce a "geometrical parameter" in the formula of the model function, in order to take into account free points existing in the geometrical calculations (t, x, or y folllowed by the identifier of the free point). The value of a geometrical parameter depends on the position of the relevant free point. By default, geometrical parameters are instanciated. If necessary, an option int the Option window allows  (de)instanciating like the other parameters. See onlinehelp.