The algebra tab



The four lists in the algebra tab

The list of expressions

Each function or expression can appear with one or several formulae : there must be one initial formula, chosen by the user or calculated by Casyopee. Other equivalent forms (developed, factorized, reduced to the same denominator, decomposed into simple elements) being obtained by calculation.

 The List of the values of the variable

This is the ordered list of values of the variable for a given identifier (eg. x) involved in the study. It appears optionnaly, together with the list of functions.

These values appear in other dialog boxes and in the statement of properties of functions. By default the identifier is x.

The user can introduce new values into the list with the NewValue Button or when entering the the set of definition of functions. Each new value appears with its identifier: example x0 = 1 if the first created value is 1. In case of a zero obtained by the theory of bijection, only the identifier appears.

The List of functions

This is the  list of functions for a given identifier (eg. x). It appears optionnaly, together with the List of the values of the variable

Each function appears with its identifier and a table of properties (definition, zero, discontinuity, sign, monotonicity) which can be copied in the notepad. Some functions are created by the user. Their identifier is a letter (f, g...) which can be used to create new objects. Other functions are calculated. Their identifier are formed from the one of the initial function (f’ for the derivative of f, f0 for a sub-expression of f...) and can be used to create new objects. PieceWise functions and fonctions defined by an algorithm also appear in this list.

The List of Equations

To start solving an equation, it must be selected. A box will appear to the right of the list. Depending on the type of equation, several options are available.
The dropdown menus exact / approximate: in case of a numerical equation.
Unknown: choose an unknown among the different parameters of the equation (available for an equation of the form 0 = K).

Approximate Resolution
In the case of an approximate resolution, the Newton's algorithm is used. In the case where the variable is unknown, the algorithm starts at the value of the trace on the graph. In the case when the unknown is a parameter, the algorithm starts at the current value. In both cases, it is interesting to choose a value close to the conjectured solution.
See Online Help.

The algebra tab menu

Evaluate formula

It is often useful to evaluate a formula, either by way of symbolic calculation or by numerical approximation, without storing the result. An entry box opens. Various transformations are offered. The result is displayed in the NotePad and can be copied in various formats. See Online Help.

Create Expression

This command creates an expression. See Online Help.

The entry box has a menu , buttons and a text entry form for a formula.

Edit: This menu offers actions Copy (Ctrl + C), Cut (Ctrl + X) and Paste (Ctrl + V).

The text entry form: it can be filled through buttons in bands or using the keyboard and remove a selection in the formula by the button. The formula can be defined using parameters. Formulae are like on claclulators, for example, to write powers, use the sign "^". So to write a² it should be noted "a ^ 2". Multiplication is implicit. If you enter a not already used letter Casyopee proposes to create a parameter. The Edit menu offers the actions Copy (Ctrl + C), Cut (Ctrl + X) and Paste (Ctrl + V). A drop-down menu allows to reuse a formula written before.

Dropdown names list. Left to the Create button this is used to select the name of the expression. In Casyopee, all objects have a name, which is composed of an alphabetic character.

Create: Saves the expression in the list of expressions. The expression appears then in the expressions list.
Exit: Close the input box

Create Function

This menu allows creating various functions. The function appears then in the functions list, and its formula in the expressions list.

By formula

In addition to the Create Expression box, the dialog box has a button for entering a variable identifier . Note that multiple identifiers are possible, x being proposed by default. Also note that like with expressions, it is possible to ask Casyopee to check if the function is well defined for all real (checkbox Check Existence). If this verification is made, the function will be placed in the list of functions.

Other inputs and buttons are the same as in the Create Expression box.

By formula and domain

The entry box has an additional input field to enter the domain (or  set of definition of  a function). It must be entered in the usual mathematical syntax. This input field is accompanied by two buttons
Evaluate
Determines whether the set of definition is correctly entered and creates the values of the corresponding variable. You have to click this button before accessing the "Create" button.
Auto
Casyopee computes the set definition by using the values of existing variables.
If you checked "Checking existence", Algebra tab now includes a list of x values and a mini table for functions whose domain has been verified ..
See Online Help

By an algorithm

Documentation here

PieceWise

This command creates a new function defined by intervals. See Online Help.

Create Equation

This command creates an equation.

This one appears then in the equations list.

Contextual Menu

The contextual menu of the objects in the algebra tab mirrors the Edit entry of the main menu. In addition, when the object depend on parameters, the menu offers to instantiate or deinstantiate the parameters in the object. When possible, this menu gives also an approximate numerical value, from the current value of the object.See Online Help.

Button Calculate

The button Calculate allows to apply calculations on the expression selected in the expressions list. See Online Help.

Statute, modification of an expression

This command sends a message indicating how the expression was obtained. In cas it is the initial formula of an expression or a function (not derived) a box proposes to modify the formula. The changes are executed on all dependent objects.

Substitute a parameter

This command is applied only to an expression written with the help of parameters.

This is available in the menu Calculate, when some parameters are instanciated.

To substitute a parameter in a selected expression.

  1. One chooses the value to substitute with the help of the cursor of command of parameter,

  2. then one selects the command in the menu Calculate.

  3. A window asks confirmation

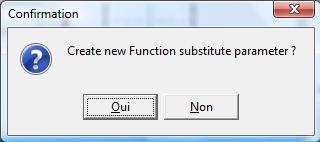
  4. A new expression and possibly, a new function are then added into the list of’expressions and of functions.

Partial Fractional Expansion

This command is applied to a selected expression.

This one allows to decompose a rational fraction into simple elements.

The decomposition is written in the notepad.

When the found expression is not yet in the expressions list, a window suggests to add it into the list.

Factorization

This command is applied to a selected expression.

This one allows to factorize a polynomial in R as well as the numerators and denominators of a rational function. When the roots of the polynomial are irrational, they have to be in the list of variable in order to find the corresponding factorization. The command Zeros allows to obtain this roots.

The factorization is written in the notepad.

When the found expression is not yet in the expressions list, a window suggests to add this one into the list.

Expand

This command allows to develop a selected expression.

The expansion is written in the notepad.

When the found expression is not yet in the expressions list, a window suggests to add this one into the list.

Reduction to the common denominator

This command allows to reduce an expression comprising quotients to the same denominator.

The reduced expression is written in the notepad.

When the found expression is not yet in the expressions list, a window suggests to add this one into the list.

Derivative

This command is applied to a selected expression of a function.

This one allows to calculate the derivative of the function corresponding to the expression.

The derivative function is added to the list functions list, its developed formula is added to the expressions list.

Primitive

This command is applied to a selected expression of a function.

This one allows to calculate a primitive of the function.

The primitive is added to the functions list, its developed expression is added to the expressions list.

Zeros

This command is applied to a selected expression of a function.

It allows to determine the real numbers whose the images by the function corresponding to the expression are equal to 0.

The number of real and possible solutions as well as the solutions belongs to the set of definition of the function are written in the notepad.

When the found solution is not yet in the variable value list, a window suggests to add it into the list.

If the values are irrational zeros of a function, the factorized form of the function can be modified in order to include new factors.

Button Justify

The menu opened by the Justify button offers a set of commands for algebraic proof of properties of the selected function. The properties deal with signs or monotonicity on intervals.The justifications start by a “ conditions of application ” dialog box. The various theorems and boxes are detailed below.

It is followed the Conclusions dialog box which is to be completed. The list of intervals delimited by the variable values on which the function is defined is displayed. For each one of intervals, the user can complete while proposing a sign by click in the right box. A button  allows  the software to verify the consistence with conclusions of the in-progress justification.The conclusions are then copied in the notepad and appear in the table of properties of functions. See Online Help.

Signs: Linear

Theorem

a linear function x -> ax + b, of no null coefficient is of sign of -a in ] -∞ , -b/a ] and of sign of a in [ -b/a , +∞ [.

In the dialog box, the Evaluate button verifies the equality between the function to justify and the affine function whose the coefficient of x and of the value for which the function is equal to 0 have been entered.

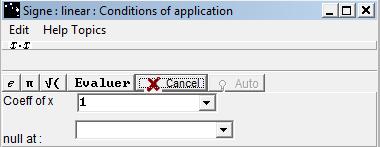
If the evaluation is positive, the Conclusions dialog box shows up.

Signs: Second degree

Theorem

a trinomial of second degree x -> ax² + bx + c (where a is no null) being equal to 0 on x1 and x2 is at the same sign of -a in [x1, x2] and at the same sign of a in ] -∞ , x1 [ and in ] x2 , +∞ [.

The Evaluate button verifies the equality between the current function and the second degree function whose the coefficient of x² and the values for which the function is equal to 0 have been entered.

In case of a negative discriminant, the second tab allows to justify that the function is the sign of coefficient.

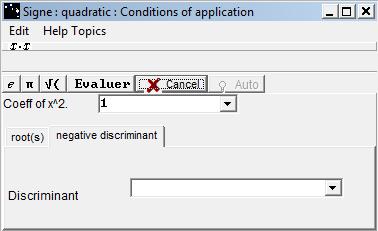
If the evaluation is positive, the Conclusions dialog box shows up.

Signs: Product, quotient

theorem

The product of two functions of the same sign is positive, the product of two functions of the opposite sign is negative.

When it is defined, the quotient of two functions of the same sign is positive, the quotient of two functions of opposite sign is negative.

A list of functions for which the sign is known on an interval is given. One selects in this list the functions necessary to the study of the sign of the current function.

The Evaluate button verifies if the function is equal or to the product of selected functions in the list or not, with a constant factor of difference.

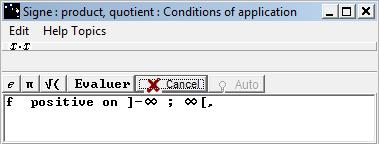
If the evaluation is positive, the Conclusions dialog box shows up.

Signs: Sum

Theorem

The sum of functions of the same sign is the sign of functions.

A list of functions for which the sign is known is given.

The Evaluate button verifies the equality, with a constant factor of difference, between the function and the sum of selected functions in the list.

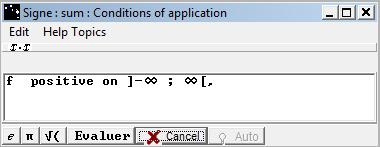
If the evaluation is positive, the Conclusions dialog box shows up.

Signs: Monomial

Theorem

the functions x -> ax^(2n) are the sign of a on R, the functions x -> ax^(2n+1) are the sign of a on R+ and are the sign of -a on R-.

The Evaluate button verifies the equality of between the function to justify and the monomial function whose the coefficient and the degree have been entered.

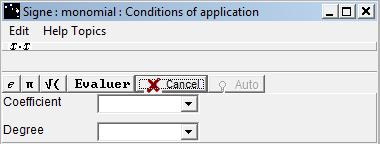
If the evaluation is positive, the Conclusions dialog box shows up.

Signs: Inverse

Theorem

The sign of the inverse of a function not null is the one of the function.

A list of functions whose the sign is known on an interval is given.

The Evaluate button verifies the equality between the function to justify and the inverse function of the selected function in the list.

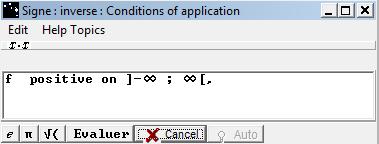
If the evaluation is positive, the Conclusions dialog box shows up.

Signs: Square, root, absolute value.

Theorem

The composite of a function of reference with every defined function f is positive.

The dialog box suggests to choose of positive function of reference (on an interval known) and to enter an expression (possibly in a list of sub-expression).

The Evaluate button verifies if, by a constant factor of difference, the function to justify is equal to the function defined by the selected function of reference and by the entered expression

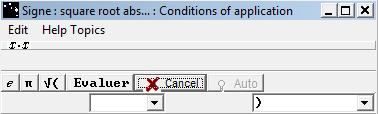
If the evaluation is positive, the Conclusions dialog box shows up.

Signs: Known Variations

Theorem

  • In the case of an increasing function on an interval

    • If this function has a value[*] which is positive at the left bound, this function is positive on the interval.

    • If this function is equal to 0 at a point of the interval, the function is negative on the left of this point and positive on the right.

    • If this function has a value [*] negative on the right bound, the function is negative on the interval.

  • In the case of a function decreasing on an interval

    • If this function has a value [*] negative on the left bound, the function is negative on the interval.

    • If this function is equal to 0 at a point of the interval then the function is positive on the left of this point and negative on the right.

    • If this function has a value [*] positive on the right bound, the function is positive on the interval.

A list of intervals, as well as the intervals of monotonicity of the function to be justified are displayed.

The user can select every interval in the list.

The list of variable values of the interval is given. It's possible to select one of these values and to indicate the sign of the value of the function. The software verifies the validity of the sign.

The Evaluate button verifies the applicability of the theorem on each one of selected intervals.

If at least one of evaluations is positive, the Conclusions dialog box is displayed.

Variations: Known derivative sign

theorem

If the derivative of a derivable function is positive on an interval then the function is increasing on this interval. If the derivative of a derivable function is negative on an interval then this function is decreasing on this interval.

A list of function whose the sign is known on an interval is given.

The Evaluate button verifies if the function to justify admits the selected function in the list as derivative.

Zeros: Intermediate value theorem

Theorem

if a function continuous and strictly monotone on an interval has different signs at the bound of this interval then this function has one and only one zero belonging to this interval.

This command allows to justify the existence of a zero of a function in particular when one can not determine a exact zero by calculation: theorem of intermediate values in case of a strictly monotone function.

The user selects the function in the list then clicks on the right button, selects justification of intervals of monotonicity and then "Zeros of a continuous and strictly monotone function"

A dialog box is opened : the user gives the intervals of monotonicity in the interval. The button "evaluate" of Casyopee verifies the equivalence between the expression and the studied function.

The zero is displayed in the table of the functions list and in the notepad under the written form.